2 data representation, Data representation -12, Section 4.3.2, “data – Freescale Semiconductor MCF5480 User Manual
Page 160: Representation, Value 1 a
MCF548x Reference Manual, Rev. 3
4-12
Freescale Semiconductor
The mov.l instruction that stores the accumulator to an integer register (Rz) stalls until the program-visible
copy of the accumulator is available.
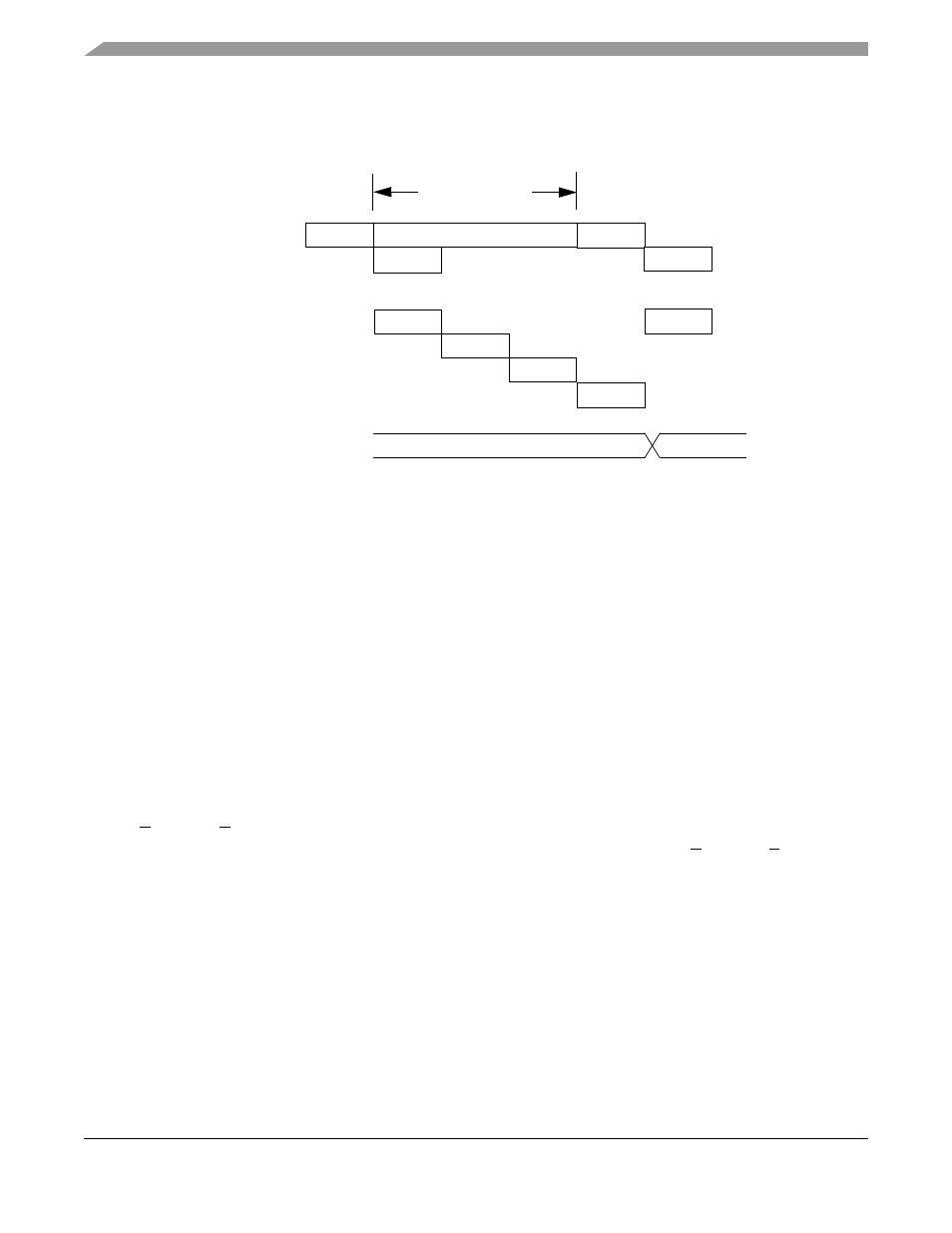
shows EMAC timing.
Figure 4-8. EMAC-Specific OEP Sequence Stall
In
, the OEP stalls the store-accumulator instruction for 3 cycles: the depth of the EMAC
pipeline minus 1. The minus 1 factor is needed because the OEP and EMAC pipelines overlap by a cycle,
the AGEX stage. As the store-accumulator instruction reaches the AGEX stage where the operation is
performed, the just-updated accumulator 0 value is available.
As with change or use stalls between accumulators and general-purpose registers, introducing intervening
instructions that do not reference the busy register can reduce or eliminate sequence-related store-MAC
instruction stalls. In fact, a major benefit of the EMAC is the addition of three accumulators to minimize
stalls caused by exchanges between the accumulator(s) and the general-purpose registers.
4.3.2
Data Representation
MACSR[S/U,F/I] selects one of the following three modes, where each mode defines a unique operand
type:
•
Two’s complement signed integer: In this format, an N-bit operand value lies in the range -2
(N-1)
< operand < 2
(N-1)
- 1. The binary point is right of the lsb.
•
Unsigned integer: In this format, an N-bit operand value lies in the range 0 < operand < 2
N
- 1. The
binary point is right of the lsb.
•
Two’s complement, signed fractional: In an N-bit number, the first bit is the sign bit. The remaining
bits signify the first N-1 bits after the binary point. Given an N-bit number, a
N-1
a
N-2
a
N-3
... a
2
a
1
a
0
,
its value is given by the equation in
Figure 4-9. Two’s Complement, Signed Fractional Equation
DSOC
AGEX
mac
mac
EMAC EX1
EMAC EX2
EMAC EX3
EMAC EX4
mac
mac
mac
mac
mov
mov
mov
mov
Three-cycle
regBusy stall
Accumulator 0
old
new
value
1 a
N 1
–
⋅
(
)
–
2
i 1 N
–
+
(
)
ai
⋅
i
0
=
N 2
–
∑
+
=
