Rockwell Automation 1784-PM16SE SoftLogix Motion Card Setup and Configuration Manual - Manual (Page 284)

Publication 1784-UM003A-EN-P – June 2003
276 Motion Object Attributes
Registration Position Two registration position attributes are provided to independently store axis
position associated with two different registration input events. The
Registration Position value is the absolute position of a physical or virtual axis
(in the position units of that axis) at the occurrence of the most recent
registration event for that axis.
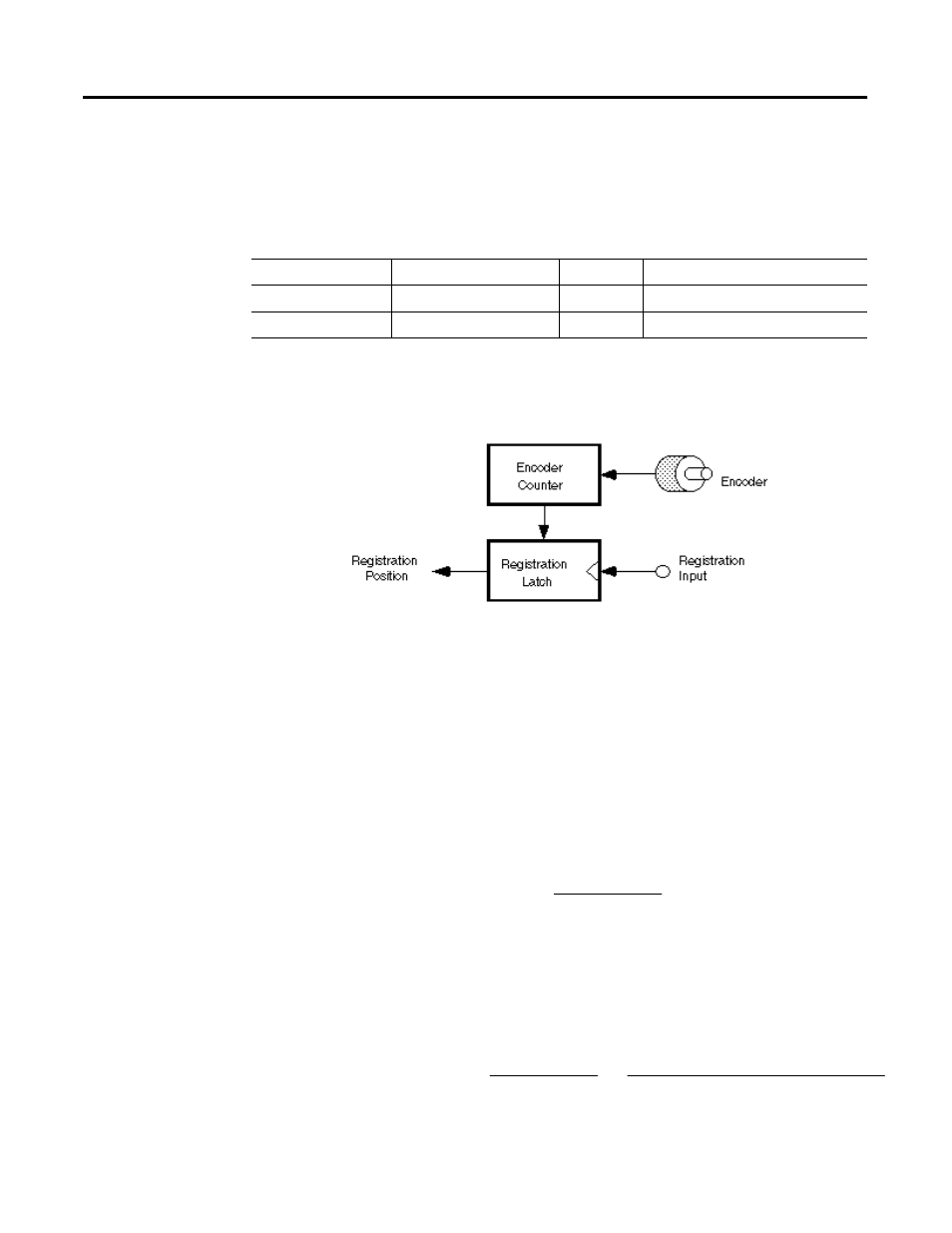
The figure below shows how the registration position is latched by the
registration input when a registration event occurs. The latching mechanism
can be implemented in the controller software (soft registration) or, for greater
accuracy, in physical hardware (hard registration).
Figure 13.2 Registration Position
The Registration Latch mechanism is controlled two Event Control
instructions, MAR (Motion Arm Registration) and MDR (Motion Disarm
Registration). Refer to the AC Motion Instruction Specification for a detailed
description of these instructions.
The accuracy of the registration position value, saved as a result of a
registration event, is a function of the delay in recognizing the specified
transition (typically 1 µsec. for hardware registration) and the speed of the axis
during this time. The uncertainty in the registration position is the distance
traveled by the axis during this interval as shown by the equation below:
Use the formula given above to calculate the maximum registration position
error for the expected axis speed. Alternatively, you can calculate the maximum
axis speed for a specified registration accuracy by re-arranging this formula as
shown below:
GSV/SSV Access Attribute Name Data Type Values
GSV Registration 1 Position REAL Position Units
GSV Registration 2 Position REAL Position Units
Delay
Second
Units Position
Speed Axis Uncertain ty
×
⎥⎦
⎤
⎢⎣
⎡
=
[ ]
Delay
Units Position Accuracy Desired
Second
Units Position
Speed Maximum =
⎥⎦
⎤
⎢⎣
⎡