Metrohm viva 1.1 (ProLab) - Manual (Page 709)

￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭
5 Method
viva 1.1 (for process analysis)
￭￭￭￭￭￭￭￭ 697
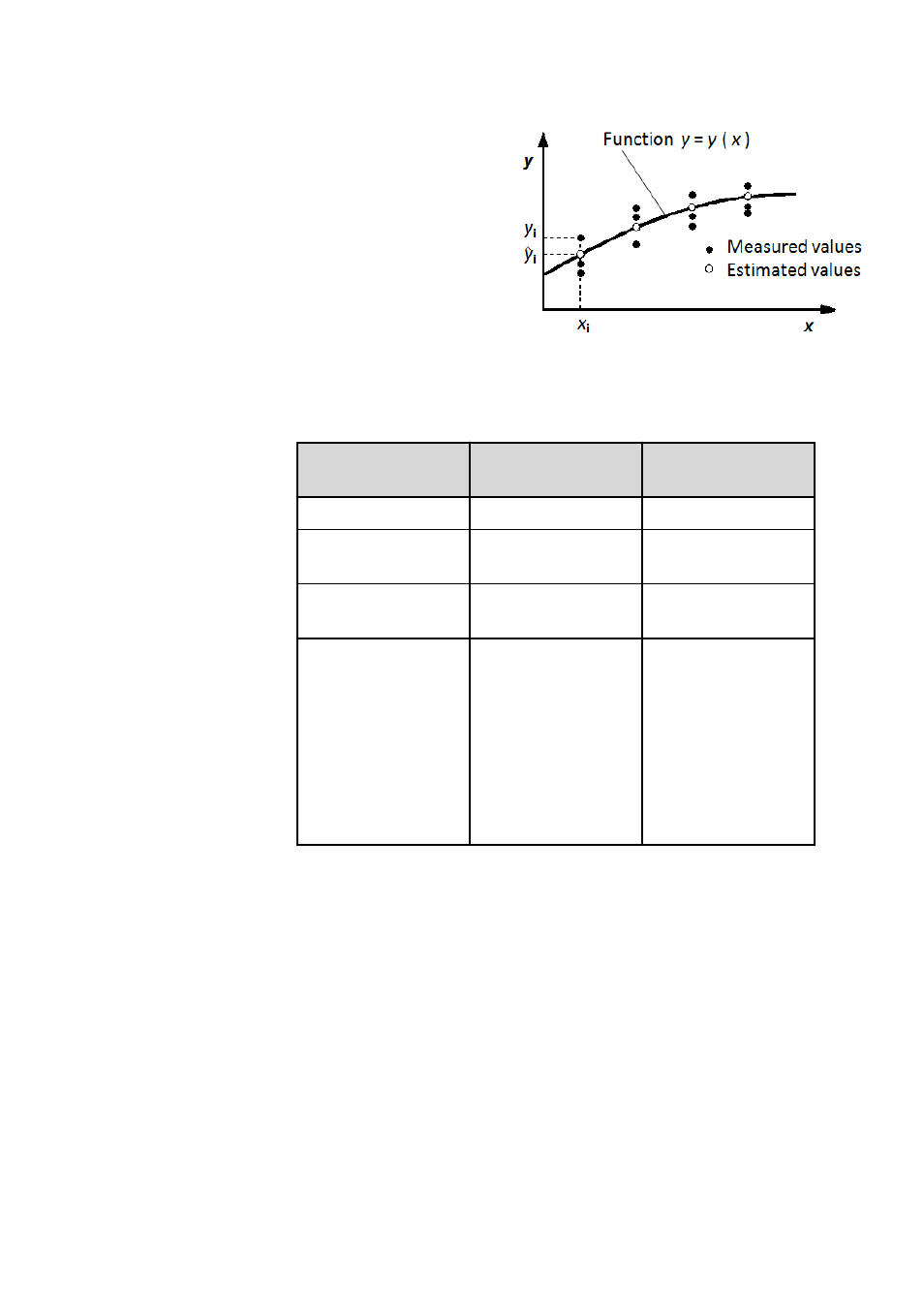
￭ The variable x is error-
free.
￭ The variable y is depen-
dent on x and can be
described by the func-
tion y = y(x).
￭ The error with the mea-
surement of y is distrib-
uted normally and is
sufficiently small to be
able to apply linear
error calculation.
Depending on the calibration method selected, the following model func-
tions are available for the calculation of the calibration curve y = y(x):
Selected curve type Calibration func-
tion
Description
Linear regression y = a + bx Line
Quadratic regres-
sion y = a + bx + cx 2 Nonlinear curve of
the 2nd degree
Nonlinear regres-
sion y = a + bx + dx 4 Nonlinear curve of
the 4th degree
Linear interpola-
tion y = a + bx Line for which all rep-
lications of the two
standard solutions
which are closest in
size to the measured
value of the sample
are taken into
account by the cali-
bration curve.
To calculate the parameters a, b, c and d, the Least Squares Fit method is
applied, for which the sum of the squared deviations of the measured val-
ues y
i
from the estimates
ŷ
i
is minimized. The scatter σ
y,i
of the measured
values is usually not constant, however, but rather dependent on its value.
It is for that reason that the deviations can be weighted with a factor of
g
i
. Extremely scattered values should be given less weight, more precisely
measured values should be weighted more heavily. It is known from statis-
tics that, under the conditions listed, weighting 1/variance = 1/standard
deviation
2 = 1/( σ
y,i
) 2 yields the best results. In practice, however, the num-
ber of repeated measurements is too low to allow estimates from the
measured values
σ to be made. A general fact is of help here: