Delta DVP-ES2 - Manual (Page 524)

D V P - E S 2 / E X 2 / S S 2 / S A2 / S X 2 O p e r a t i o n M a n u a l - P r o g r a m m i n g
3 - 4 0 8
Points to note:
1. A matrix consists of more than 1 consecutive 16-bit registers. The number of registers is
indicated as the matrix length (n). A matrix contains 16 × n bits (points) and the matrix
instructions conduct bit operation, i.e. operation is performed bit by bit.
2. Matrix instructions designate a single bit of the 16 × n bits (b
0
~ b
16n-1
) for operation. The bits
in matrix are not operated as value operation.
3. The matrix instructions process the moving, copying, comparing and searching of
one-to-many or many-to-many matrix operation, which are a very handy and important
application instructions.
4. The matrix operation requires a 16-bit register for designating a bit among the 16n bits in the
matrix. The register is the Pointer (Pr) of the matrix, designated by the user in the instruction.
The valid range of Pr is 0 ~ 16n -1, corresponding to b0 ~ b16n-1 in the matrix.
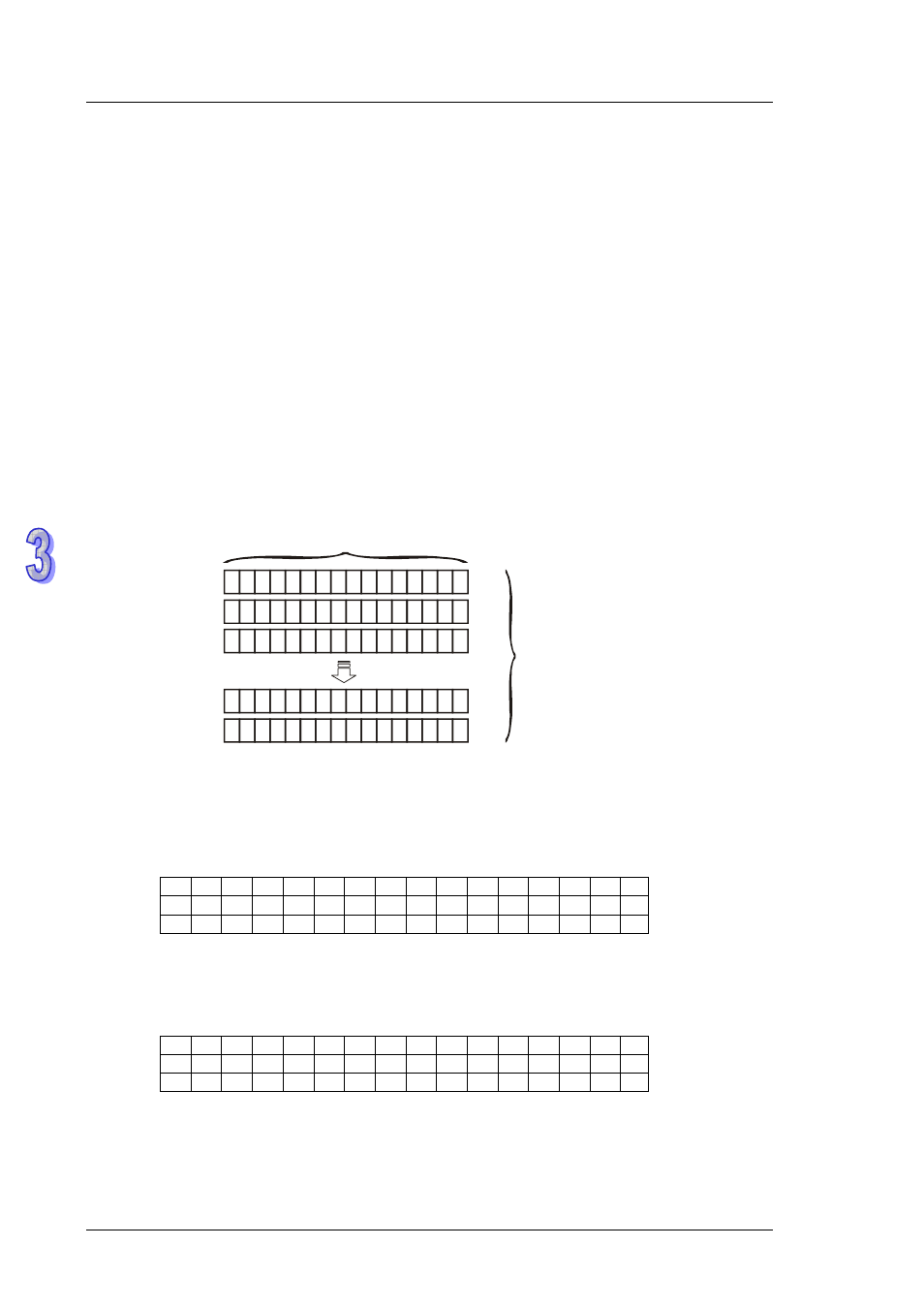
5. The bit number decreases from left to right (see the figure below). With the bit number, matrix
operation such as bit shift left, bit shift right, bit rotation can be performed and identified.
1 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1
1 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1
1 1 0 1 0 0 0 0 0 0 0 0 1 1 0 0
1 1 0 1 0 0 0 0 0 0 0 0 1 1 0 0
b0
b16
b32
b31
b15
b47
D0
D1
D2
b16n-1
1 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1
Left Right
Width: 16 bits
Dn-1
Le
n
gt
h
:
n
6. The matrix width (C) is fixed as 16 bits.
7. Pr: matrix pointer. E.g. if Pr is 15, the designated bit is b15.
8. Matrix length (R) is n: n = 1 ~ 256.
Example: This matrix is composed of D0, n = 3; D0 = HAAAA, D1 = H5555, D2 = HAAFF
C
15
C
14
C
13
C
12
C
11
C
10
C
9
C
8
C
7
C
6
C
5
C
4
C
3
C
2
C
1
C
0
R
0
1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 D0
R
1
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 D1
R
2
1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 D2
Example: This matrix is composed of K2X20, n = 3; K2X20 = H37, K2X30 = H68, K2X40 =
H45
C
15
C
14
C
13
C
12
C
11
C
10
C
9
C
8
C
7
C
6
C
5
C
4
C
3
C
2
C
1
C
0
R
0
0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 X
20
~X
27
R
1
0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 X
30
~X
37
R
2
0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 X
40
~X
47
Fill “0” into the blank in R0(C
15
-C
8
), R1(C
15
-C
8
), and R2(C
15
-C
8
).