Delta DVP-ES2 User Manual
Page 362
D V P - E S 2 / E X 2 / S S 2 / S A2 / S X 2 / S E O p e r a t i o n M a n u a l - P r o g r a m m i n g
3-246
y
PID equation for control mode k0~k2:
( )
( )
( )
S
t
PV
K
S
t
E
K
t
E
K
MV
D
I
P
*
1
*
*
+
+
=
where
MV
: Output value
P
K
: Proprotional gain
( )
t
E
: Error value
PV
(t): Present measured value
SV
(t): Target value
D
K : Derivative gain
( )
S
t
PV
: Derivative value of PV(t)
I
K : Integral gain
( )
S
t
E
1
: Integral value of E(t)
y
When
( )
t
E
is smaller than 0 as the control mode is selected as forward or inverse,
( )
t
E
will be regarded as “0"
Control mode
PID equation
Forward, automatic
E(t) = SV – PV
Inverse
E(t) = PV – SV
y
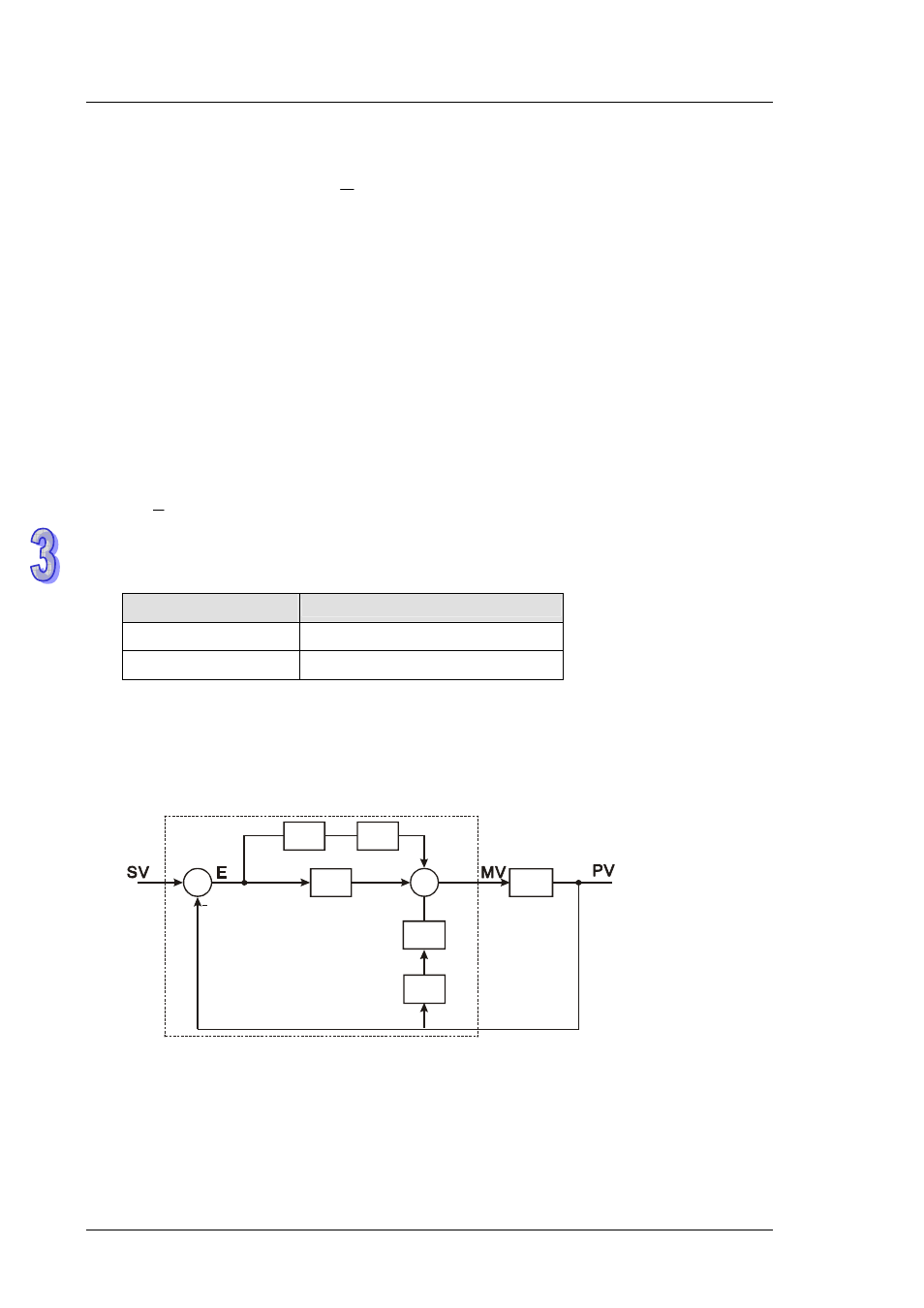
Control diagram:
In diagram below, S is derivative operation, referring to “(PV﹣previous PV) ÷ sampling time”.
1 / S is integral operation, referring to “previous integral value + (error value × sampling time)”.
G(S) refers to the device being controlled.
G(s)
S
1/S
K
I
K
P
K
D
+
+
+
PID
operation is within dotted area
+
y
The equation above illustrates that this operation is different from a general PID
operation on the application of the derivative value. To avoid the fault that the transient
derivative value could be too big when a general PID instruction is first executed, our PID
instruction monitors the derivative value of the PV. When the variation of PV is excessive, the
instruction will reduce the output of MV/.
