Delta DVP-ES2 - Manual (Page 137)

3 . I n s t r u c t i o n S e t
3 - 2 1
Binary Floating Point
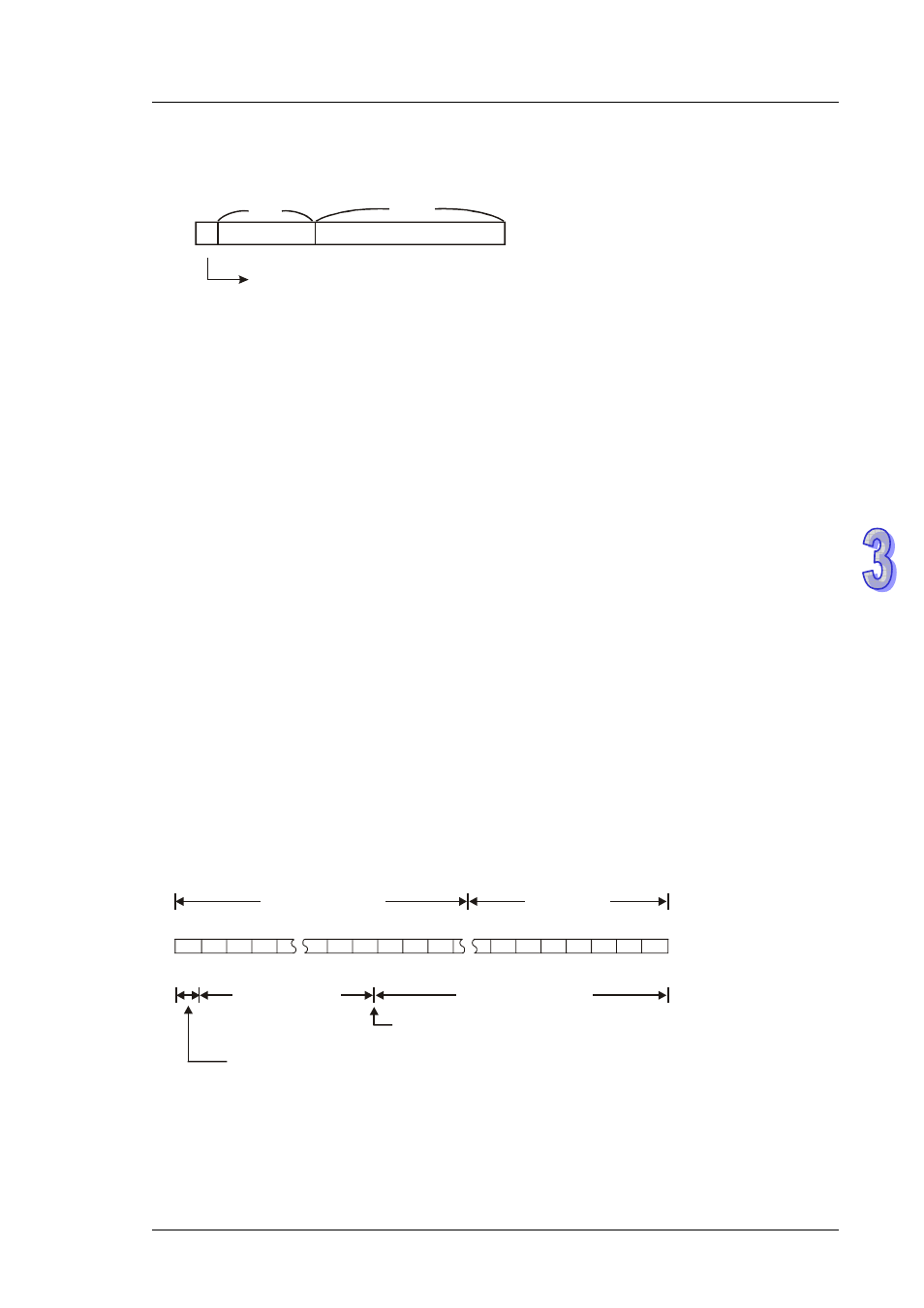
DVP-PLC represents floating point value in 32 bits, following the IEEE754 standard:
S exponent mantissa
8-bit 23-bit
b31
Sign bit
0: positive
1: negative
b0
Equation
( )
127 ; . 1 2 1
= Ч Ч − −
B M B E S
Therefore, the range of 32-bit floating point value is from ±2 -126 to ±2 +128 , i.e. from ±1.1755×10 -38 to
±3.4028×10
+38
.
Example 1: Represent “23” in 32-bit floating point value
Step 1: Convert “23” into a binary value: 23.0 = 10111
Step 2: Normalize the binary value: 10111 = 1.0111 × 2
4
, in which 0111 is mantissa and 4 is
exponent.
Step 3: Obtain the exponent: ∵ E – B = 4 E – 127 = 4 ∴ E = 131 = 10000011
2
Step 4: Combine the sign bit, exponent and mantissa into a floating point
0 10000011 01110000000000000000000
2
= 41B80000
16
Example 2: Represent “-23.0” in 32-bit floating point value
The steps required are the same as those in Example 1 and only differs in modifying the sign bit
into “1”.
1 10000011 01110000000000000000000
2
=C1B80000
16
DVP-PLC uses registers of 2 continuous No. to store a 32-bit floating point value. For example,
we use registers (D1, D0) for storing a binary floating point value as below:
S E7 E6 E5 E1 E0 A22 A21 A20 A6 A5 A4 A3 A2 A1 A0
b0 b1 b2 b3 b4 b5 b6 b20 b21 b22 b23 b24 b28 b29 b30 b31
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
7 6 5 1 0 -1 -2 -3 -17 -18 -19 -20 -21 -22 -23
D1(b15~b0) D0(b15~b0)
8 bits of exponent 23 bits of mantissa
Sign bit (0: positive 1: negative)
When b0~b31 is 0, the content is 0.
Hidden decimal point
Decimal Floating Point
Since the binary floating point value is not very user-friendly, we can convert it into a decimal
floating point value for use. However, please note that the floating point operation in DVP-PLC is
still operated in binary floating point format.