HEIDENHAIN TNC 407 (280 580) User Manual User Manual
Page 82
4-23
TNC 425/TNC 415 B/TNC 407
4
Programming
Three-Dimensional Tool Compensation (not on TNC 407)
A vector always has
• a magnitude (e.g. a distance) and
• a direction (e.g. away from the workpiece)
If a vector is perpendicular ("normal") to a surface, it is called a surface-
normal vector.
The TNC can compensate small differences in tool sizes in the surface-
normal vector NX, NY, NZ. It calculates NX, NY and NZ up to an accuracy
of seven places behind the millimeter decimal point.
Target direction of the surface-normal vector
The surface-normal vectors point from the workpiece surface to the tool
datum P
T
(see Fig. 4.16 and 4.17).
P
T
lies on the tool axis. On end mills it lies on the surface of the tool end.
On spherical cutters and toroid cutters, P
T
lies at the point on the tool
axis where the curvature begins.
• The coordinates for the X, Y, Z positions and the normal vector components NX, NY, NZ must be in the same
sequence in the NC block.
• 3D compensation with normal vectors is only available for coordinates X, Y and Z.
• The TNC will not display an error message if an entered tool oversize would cause contour error.
• Machine parameter MP 7680 defines whether the postprocessor accounts for the center of sphere or the
south pole of the sphere when calculating the tool length.
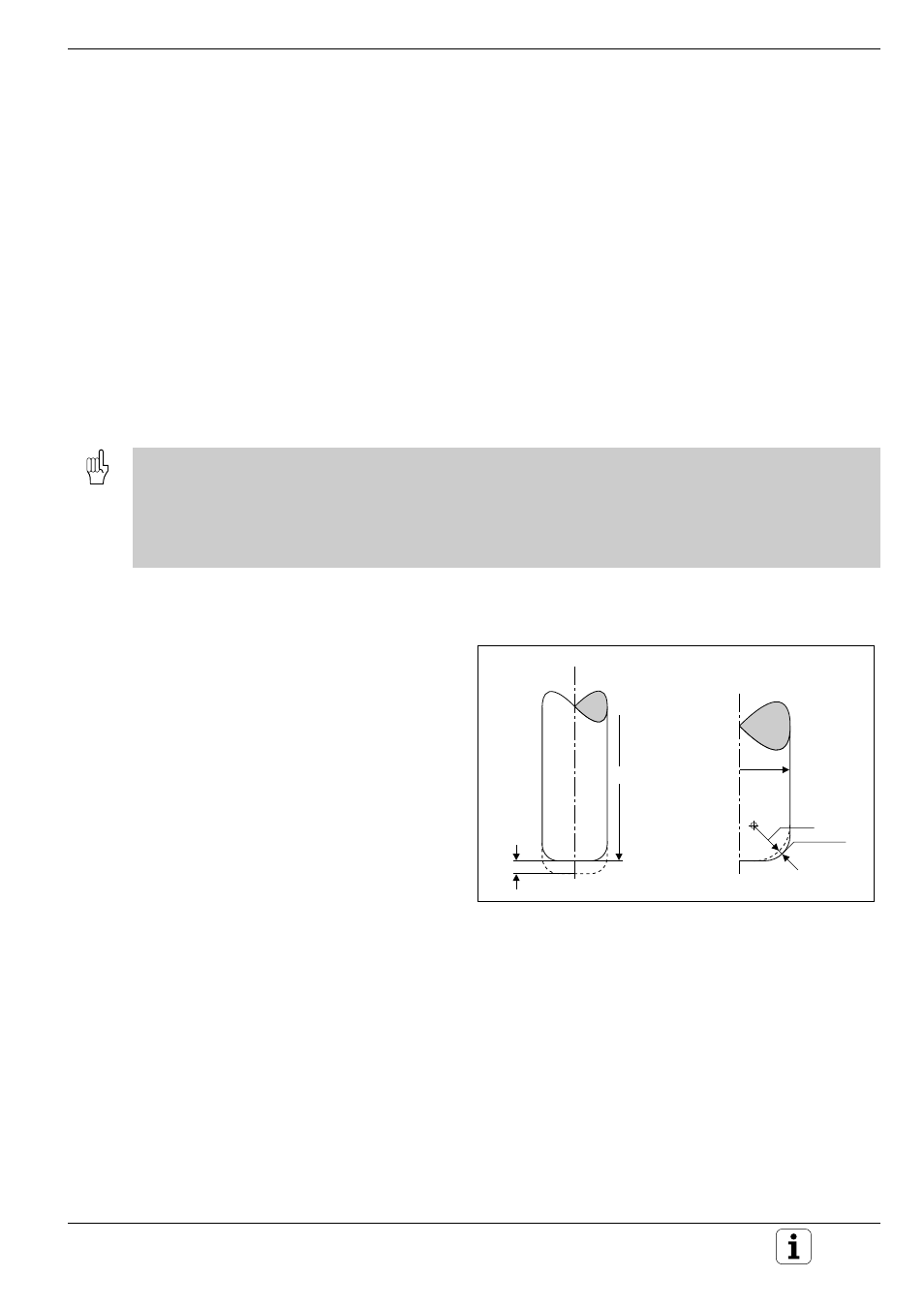
Compensating other tool dimensions by entering delta values
In some cases you may want or have to use a tool
with different dimensions than those originally
entered for 3D compensation.
You can adjust these dimensions by entering delta
values (oversize and undersize) in the tool table.
Delta values (DL for length, DR and DR2 for the
radii) can be entered up to +/– 99.999 mm (3.9 in.).
• A positive delta value is an oversize, which
means that the tool is larger than the original
tool.
• A negative delta value is an undersize, which
means that the tool is smaller than the original
tool.
The TNC corrects the tool position by the delta
values and the normal vector.
R
R2
DL>0
L
DR2>0
Fig. 4.18:
Delta values for oversize and undersize
