Appendix – Lenze Engineer v2.21 User Manual
Page 286
Appendix
Creating cam data with the »Cam Editor«
286
Lenze · Engineer · 2.13 EN - 10/2014
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
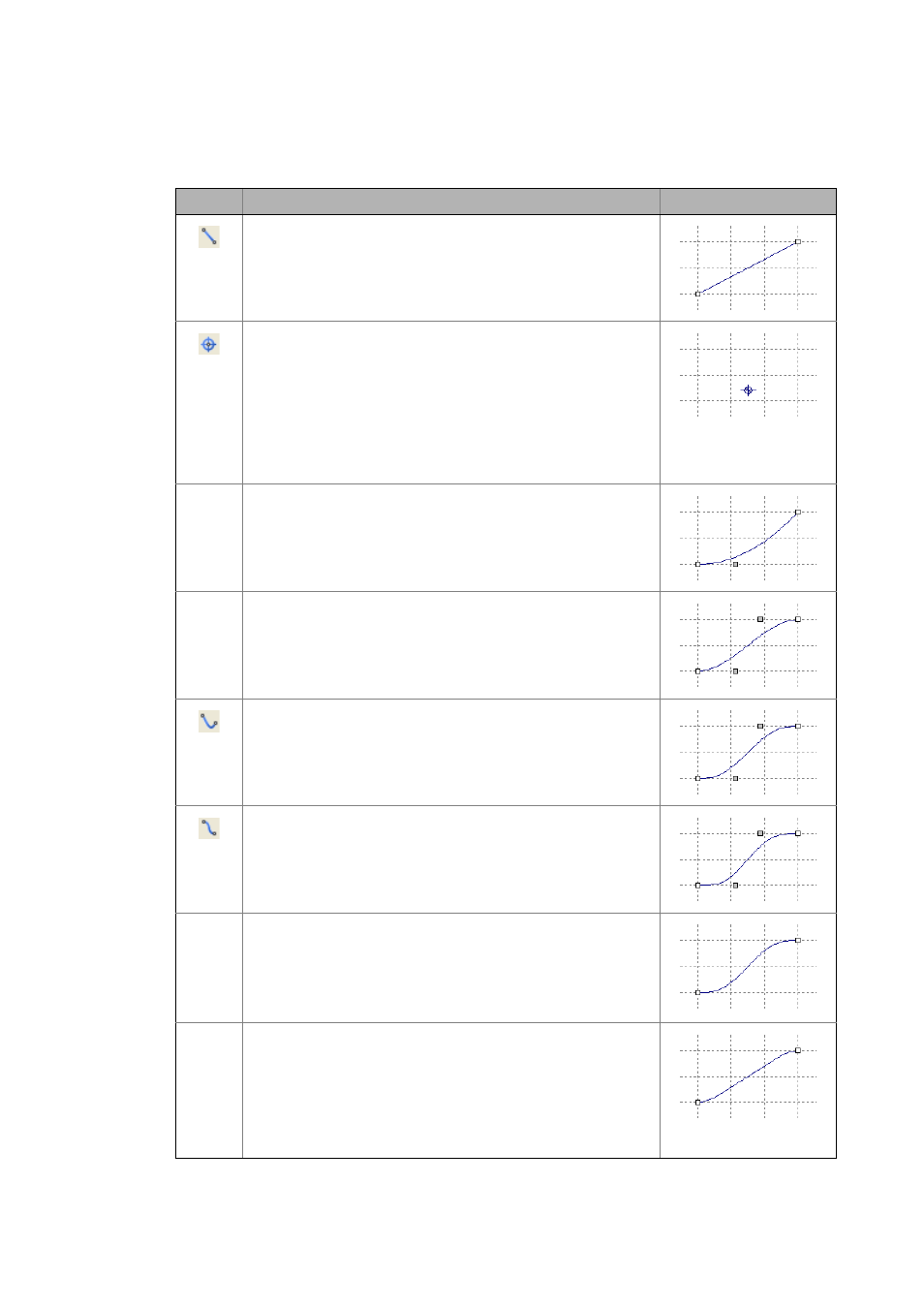
Overview of graphical objects
Icon
Object
Example
Line
The base elements stop (S) and speed (V) are defined with a line.
Point
Function is only available with »Cam Designer 3« licence upgrade.
The base elements reversal (R) and motion (M) are defined with a point.
• In the default setting, the boundary value speed has been set to "0"
for the point. This corresponds to the more frequent case of reversal
(R).
• In the default setting, the boundary value acceleration is calculated
automatically in curve mode.
• If necessary, the two boundary values can be adapted to the point in
the Properties dialog box.
-
Polynomial(2)
Function is only available with »Cam Designer 3« licence upgrade.
Second order polynomial
-
Polynomial(3)
Function is only available with »Cam Designer 3« licence upgrade.
Third order polynomial
Polynomial(5)
Fifth order polynomial
Polynomial(7)
Function is only available with »Cam Designer 3« licence upgrade.
Seventh order polynomial
-
Sloped sine line (Bestehorn)
Especially suitable for S-S (stop-stop) motion.
In the standard case, the coefficients have the following values:
A3 = 1, A2 = 1, A1 = 1, A0 = 0
-
Sine-straight line combination
Function is only available with »Cam Designer 3« licence upgrade.
Suitable for R-R (reversal-reversal) motion.
Inflection point & parameter C can be set in the Properties dialog box.
• The parameter C determines the ratio of the sine parts to the middle
part.
• At a value of 1, the middle part is equal to 0.
• The standard value is 0.5.
y
A2 x
2
A1 x
⋅
A0
+
+
⋅
=
y
A3 x
3
⋅
A2
+
x
2
A1 x
⋅
A0
+
+
⋅
=
y
A5 x
5
⋅
A4
+
x
4
⋅
A3
+
x
3
⋅
A2
+
x
2
A1 x
⋅
A0
+
+
⋅
=
y
A7 x
7
⋅
A6
+
x
6
⋅
A5
+
x
5
⋅
A4
+
x
4
⋅
A3
+
x
3
⋅
A2
+
x
2
A1 x
⋅
A0
+
+
⋅
=
y
A3 x
A2
2
π
-------
–
2
π A1 x A0
+
⋅
⋅
(
)
sin
⋅
⋅
=
