Metrohm viva 1.0 Manual - Manual (Page 605)

￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭￭
5 Method
viva 1.0
￭￭￭￭￭￭￭￭ 593
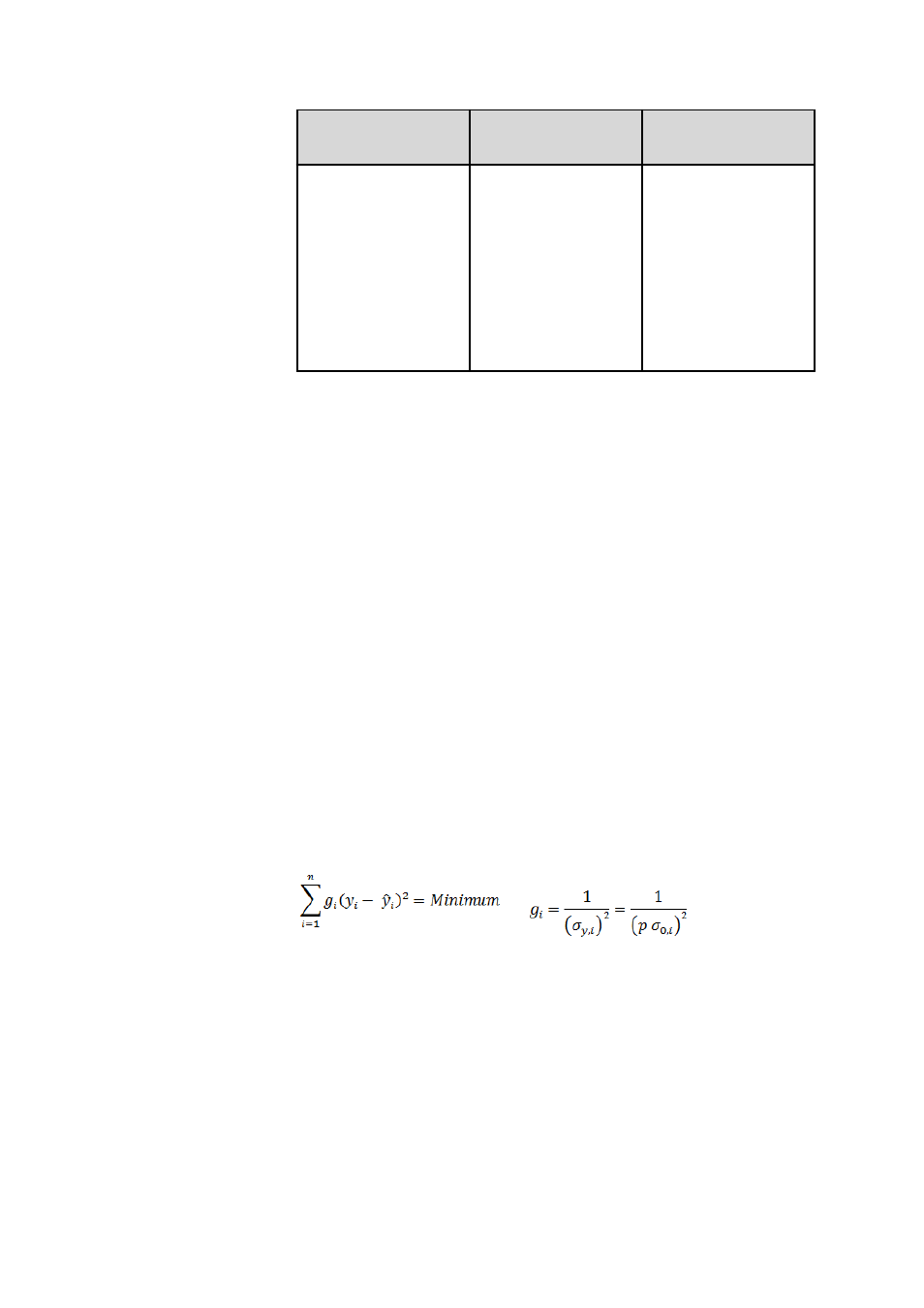
Selected curve type Calibration func-
tion
Description
Linear interpola-
tion y = a + bx Line for which all rep-
lications of the two
standard solutions
which are closest in
size to the measured
value of the sample
are taken into
account by the cali-
bration curve.
To calculate the parameters a, b, c and d, one proceeds in accordance
with the Least Squares Fit method, for which the sum of the squared devi-
ations of the measured values y
i
are minimized by the estimates
ŷ
i
. The
scatter σ
y,i
of the measured values is usually not constant, however, but
rather dependent on its value. It is for that reason that the deviations can
be weighted with a factor of g
i
. Extremely scattered values should be
given less weight, more precisely measured values should be weighted
more heavily. It is known from statistics that, under the conditions listed,
weighting 1/variance = 1/standard deviation
2 = 1/( σ
y,i
) 2 yields the best
results. In practice, however, one usually has too few repeated measure-
ments to be able to make estimates from the measured values
σ. A gen-
eral fact is of help here:
In the case of most measuring instruments, the scatter is comprised of a
constant basic part and of a part proportional to the measured quantity.
Influences that change over time also exist, however, e.g. the electrode
status or the temperature. These usually change only slowly, which is why
they can be regarded as constant during the measurement. One can
therefore take their influence into account by means of an (unknown) fac-
tor p, which is multiplied against the basic scatter. Because of the fact that
a constant factor has no influence over curve fitting, however, it can be
ignored.
with
The weighting must adopt a constant value for small measured values in
the vicinity of the instrument noise in order to exclude the possibility that
small measured values are over-weighted.
The weighting is then also appropriate if a calibration curve is acquired
across a wide concentration range. Without weighting the wide scatter of
the values with a high concentration would falsify the calibration curve for
the small values.