Motorola DSP96002 - Manual (Page 777)

MOTOROLA DSP96002 USER’S MANUAL D-25
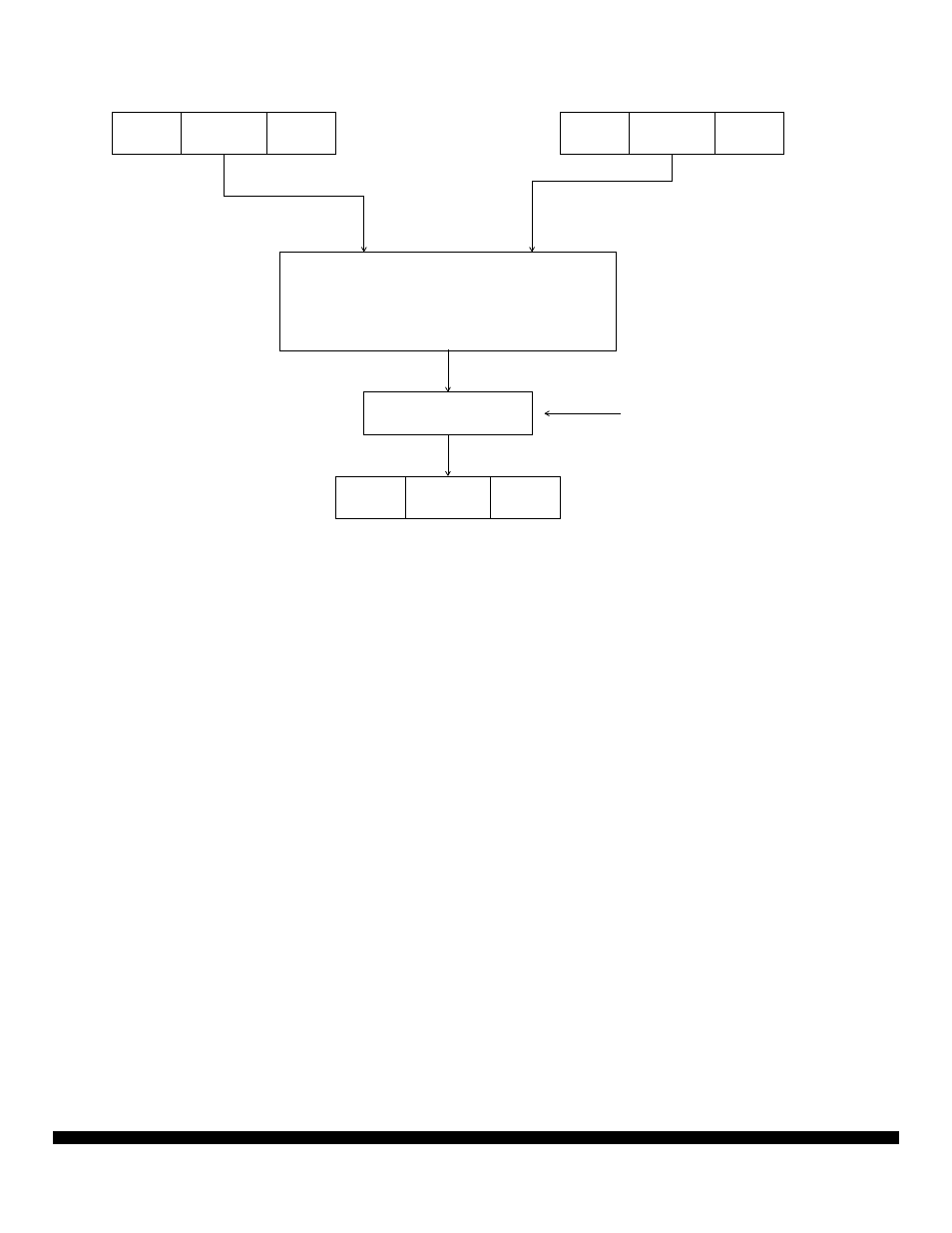
Figure D-12. The Multiply Unit
M1 M2
MD
D
32 Bits
64 Bits
32 Bits
32 Bits
Multiplier Array
Round Rounding mode is determined
by rounding bits in the MR.
this exponent for normalization of the result, after which the exponent (biased) is stored in the high portion
of the destination register. This is depicted in Figure D-16.
For example, if the mantissa of the first operand in a floating point addition is 1.010...0, with biased exponent
of 10, and the mantissa of the second operand is 1.000...0000, with biased exponent of 13, the exponent
comparator simply delivers the difference (=3) to the barrel shifter, the first operand’s mantissa is aligned to
0.001010...0, the two mantissas are added to deliver 1.001010...0, and the result (biased) exponent equals
13. The postnormalization unit does not need to postnormalize the result in this case.
If the first operand’s mantissa is 1.010...0 with biased exponent of 13 and the second operand’s mantissa
is 1.000...0 with biased exponent of 13, the exponent difference is zero and the barrel shifter does not need
to realign the mantissas. The result after addition is now equal to 10.010...0, which needs to be postnormal-
ized by adding one to the result exponent. The exponent update unit sets the result exponent (biased) equal
to 14 and the result mantissa is 1.0010...0.
Finally, if the first operand’s mantissa in a floating point subtraction is 1.010...0 with biased exponent of 10,
and the second operand’s mantissa is 1.00...0 with a biased exponent of 10, the result mantissa after sub-
traction is -0.010...0. This is not normalized, and the postnormalization unit subtracts two from the exponent.
The result mantissa is -1.000...0 with a biased exponent equal to 8.
D.1.5.4 Special Function Unit
The special function unit consists of a logic unit and a divide and square root unit. The logic unit is further
described under the fixed point (integer) operations.
The divide and square root unit supports execution of the divide and square root algorithms. These algo-
rithms are iterative, and require an initial approximation or "seed". The FSEEDD and FSEEDR instructions