Iii-1 scaling and calculating functions 91, Iii-1.1 absv (absolute value (no. 01)) 91, Iii-1.2 adsu ( addition/subtraction (no. 03)) 91 – West Control Solutions KS98-1 User Manual
Page 91: Absolute value 91, Absv 91, Addition/subtraction 91, Adsu 91, Scaling and calculating functions 91, Subtraction/addition 91, Iii-1 scaling and calculating functions
III-1
Scaling and calculating functions
III-1.1
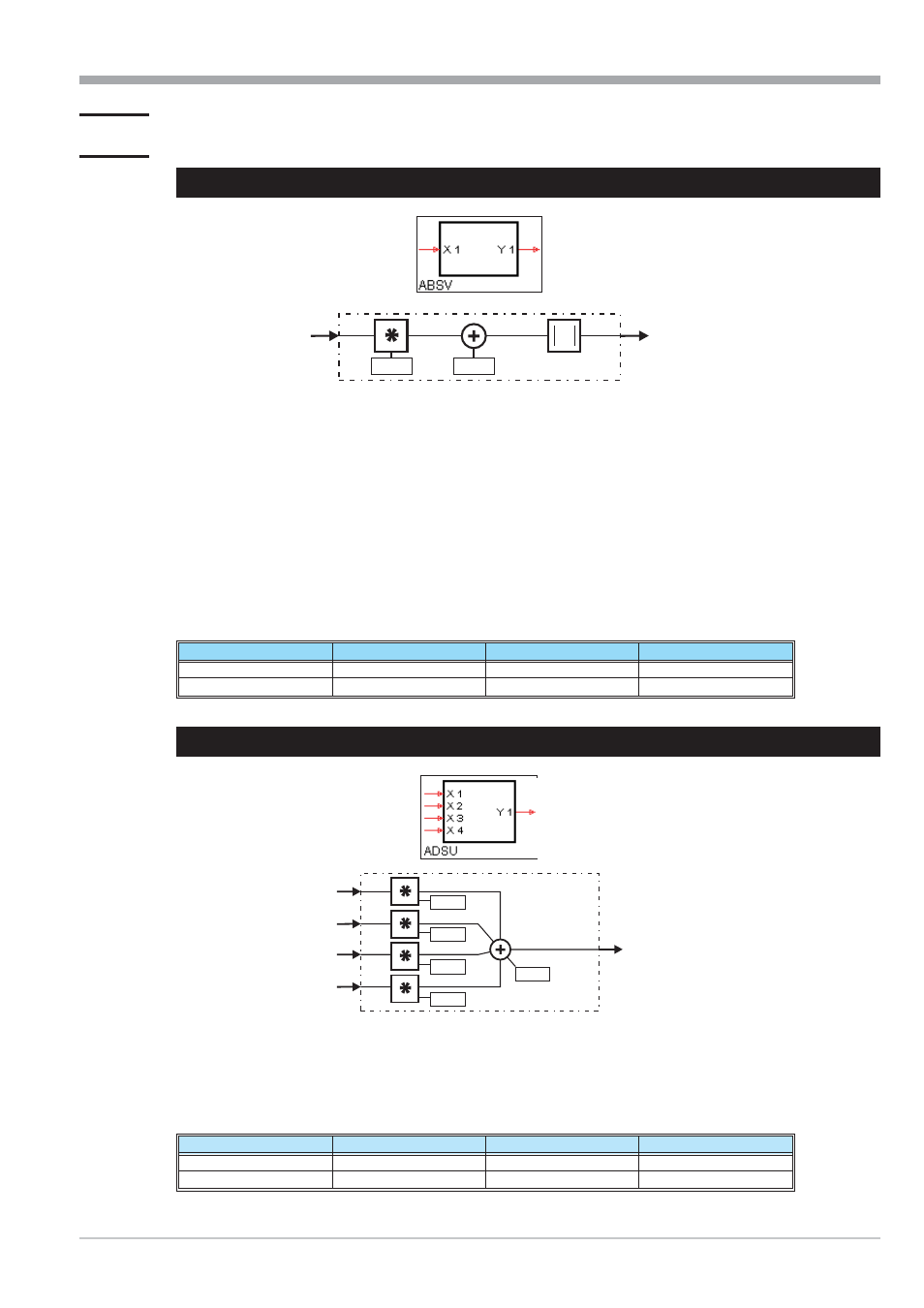
ABSV (absolute value (No. 01))
|
|
y
a x
a
1
1
0
= × +
The absolute value of a number is it's number without polarity sign. This is the best solution for scaling a value that
can't become negative, in reference to calculating time. This function block should be used, when scaling must not use
a lot of calculating time.
Input variable
x1is multiplied by factor a (parameter). Now, constant a0 is added. The absolute value of the resul-
ting value is formed and output at
y1.
Example:
y1= ABS(a w x1+ a0 ) a=5
x1=2 a0 = +5 results in y1= 15
y1= ABS(a w x1+ a0 ) a=5
x1=2 a0 = -20 results in y1= 10
Parameter
Description
Range
Default
a
Multiplication factor
-29 999...999 999
1
a0
Offset
-29 999...999 999
0
III-1.2
ADSU ( addition/subtraction (No. 03))
y
a x
b x
c x
d x
y
1
1
2
3
4
0
= Ч + Ч + Ч + Ч +
Input variables
x1...x4 are multiplied by factors a...d. Constant y0 is added to the sum of evaluated inputs. Value
“0" is assigned automatically to unused inputs.
Parameter
Description
Range
Default
a...d
Multiplication factors
-29 999...999 9990
1
y0
Offset
-29 999...999 999
0
9499-040-82711
Scaling and calculating functions
ABSV (absolute value (No. 01))
III-91
x1
A
y1
a0
a
A
x1
x2
x3
x4
y1
y0
a
c
b
d
