West Control Solutions KS98-1 - Manual (Page 125)

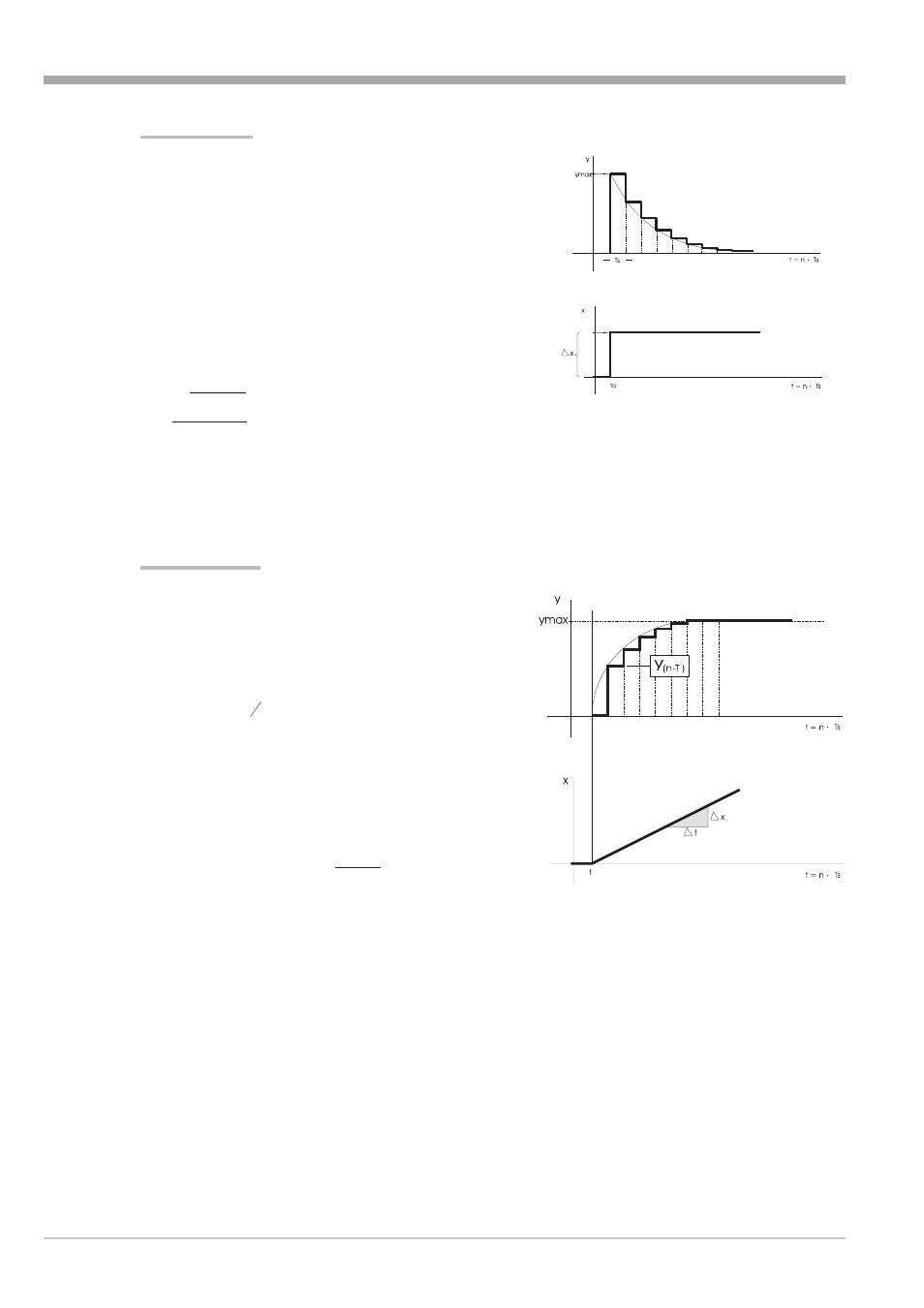
Step response:
After a step change of input variable x1 by {x =xt-x(t-ts), the
output changes to maximum value y
max.
y C a x y
max
= Ч Ч + D
0
and decays to 0 according to function
y n ts
C x y ymax C
n
n ( . ) . ( ) = Ч + = Ч - D
0 1
Thereby, n is the number of calculation cycles ts after the input
step change. Number n of required calculation cycles ts until
output variable decaying to y(n*Ts) is
n
lg
y n ts
ymax
lgC
=
×
+
( )
1
Surface area A under the decaying function is A y T ts
= × +
max
( )
Ramp response:
After ramp starting, output variable y runs towards the final
value of differentiation quotient
y m a T
max
= Ч Ч
according to function y n ts m a T C n ( ) ( )
Ч = Ч Ч Ч -
1
Thereby, m = m dx
dt
=
is the gradient factor of the input func-
tion. Relative error F after n calculating cycles Ts referred to
the final value is calculated as follows:
F = C n and the number of required calculating cycles, according
to which function y n ts ( )
× approaches final value
y= y
max
to error F is n
F
C
=
×
lg
lg 2
Time functions 9499-040-82711
III-125 LEAD ( differentiator (No. 50))
Fig. 4
s
Fig. 5