Zilog Z16C35 - Manual (Page 302)

Application Note
On-Chip Oscillator Design
15-2
OSCILLATOR THEORY OF OPERATION (Continued)
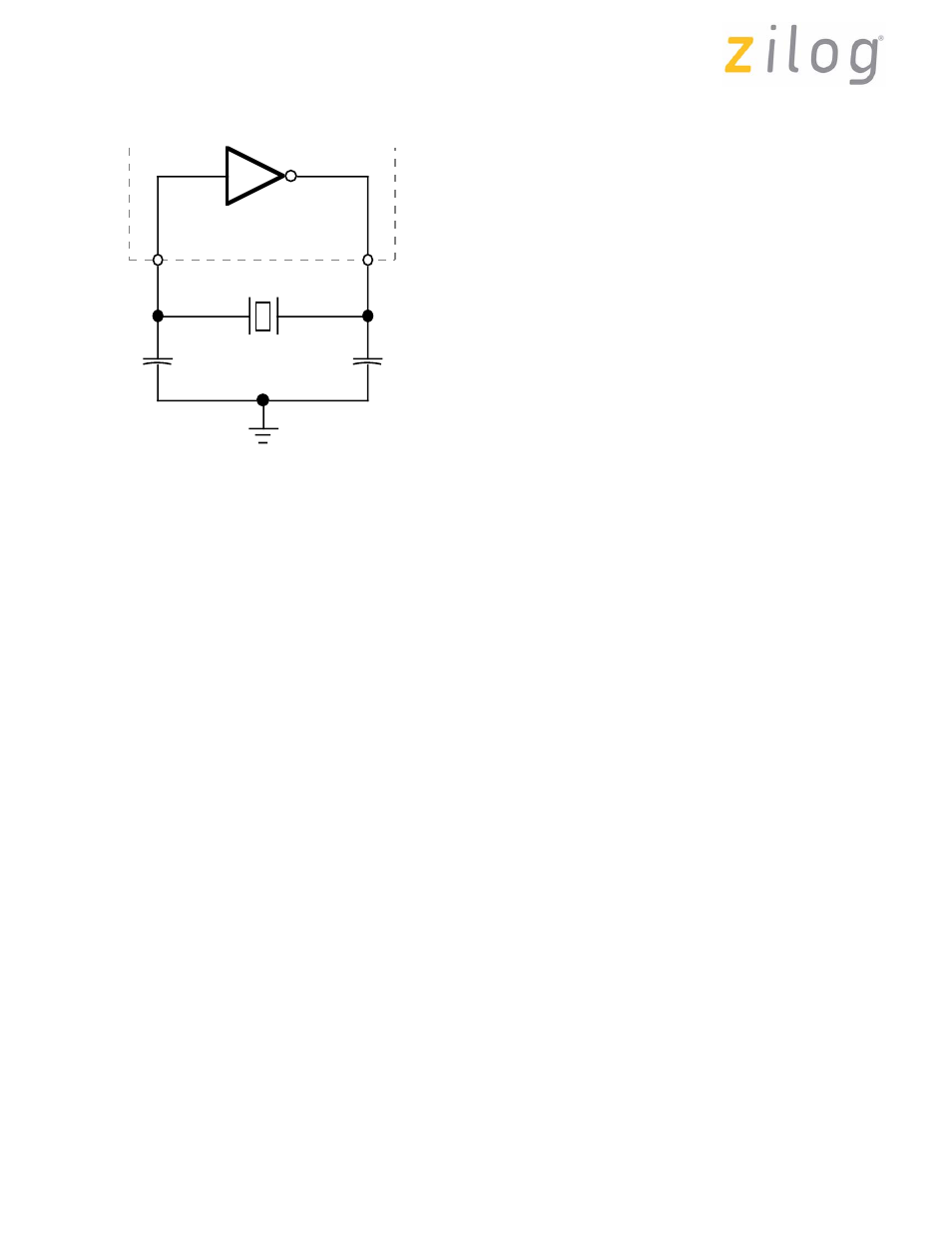
Pierce Oscillator (Feedback Type)
The basic circuit and loop gain is shown in Figure 1. The
concept is straightforward; gain of the amplifier is
A = Vo/Vi. The gain of the passive feedback element is
B = Vi/Vo. Combining these equations gives the equality
AB = 1. Therefore, the total gain around the loop is unity.
Also, since the gain factors A and B are complex numbers,
they have phase characteristics. It is clear that the total
phase shift around the loop is forced to zero (i.e., 360
degrees), since V
IN
must be in phase with itself. In this
circuit, the amplifier ideally provides 180 degrees of phase
shift (since it is an inverter). Hence, the feedback element
is forced to provide the other 180 degrees of phase shift.
Additionally, these gain and phase characteristics of both
the amplifier and the feedback element vary with
frequency. Thus, the above relationships must apply at the
frequency of interest. Also, in this circuit the amplifier is an
active element and the feedback element is passive. Thus,
by definition, the gain of the amplifier at frequency must be
greater than unity, if the loop gain is to be unity.
The described oscillator amplifies its own noise at startup
until it settles at the frequency which satisfies the
gain/phase requirement AB = 1. This means loop gain
equals one, and loop phase equals zero (360 degrees). To
do this, the loop gain at points around the frequency of
oscillation must be greater than one. This achieves an
average loop gain of one at the operating frequency.
The amplifier portion of the oscillator provides gain > 1 plus
180 degrees of phase shift. The feedback element
provides the additional 180 degrees of phase shift without
attenuating the loop gain to < 1. To do this the feedback
element is inductive, i.e., it must have a positive reactance
at the frequency of operation. The feedback elements
discussed are quartz crystals and ceramic resonators.
Quartz Crystals
A quartz crystal is a piezoelectric device; one which
transforms electrical energy to mechanical energy and
vice versa. The transformation occurs at the resonant
frequency of the crystal. This happens when the applied
AC electric field is sympathetic in frequency with the
mechanical resonance of the slice of quartz. Since this
characteristic can be made very accurate, quartz crystals
are normally used where frequency stability is critical.
Typical frequency tolerance is .005 to 0.3%.
The advantage of a quartz crystal in this application is its
wide range of positive reactance values (i.e., it looks
inductive) over a narrow range of frequencies (Figure 3).
Figure 2. Zilog Pierce Oscillator
IC
A
C1 C2
XTAL
Page 296 of 316
UM011002-0808