HEIDENHAIN TNC 426B (280 472) ISO programming - Manual (Page 130)

114 6 Programming: Programming Contours
6.5 P
ath Cont
ours — P
olar Coor
dinat
es
X
Y
40=I
35=J
30°
120°
R30 R25
Y
X
Z
I,J
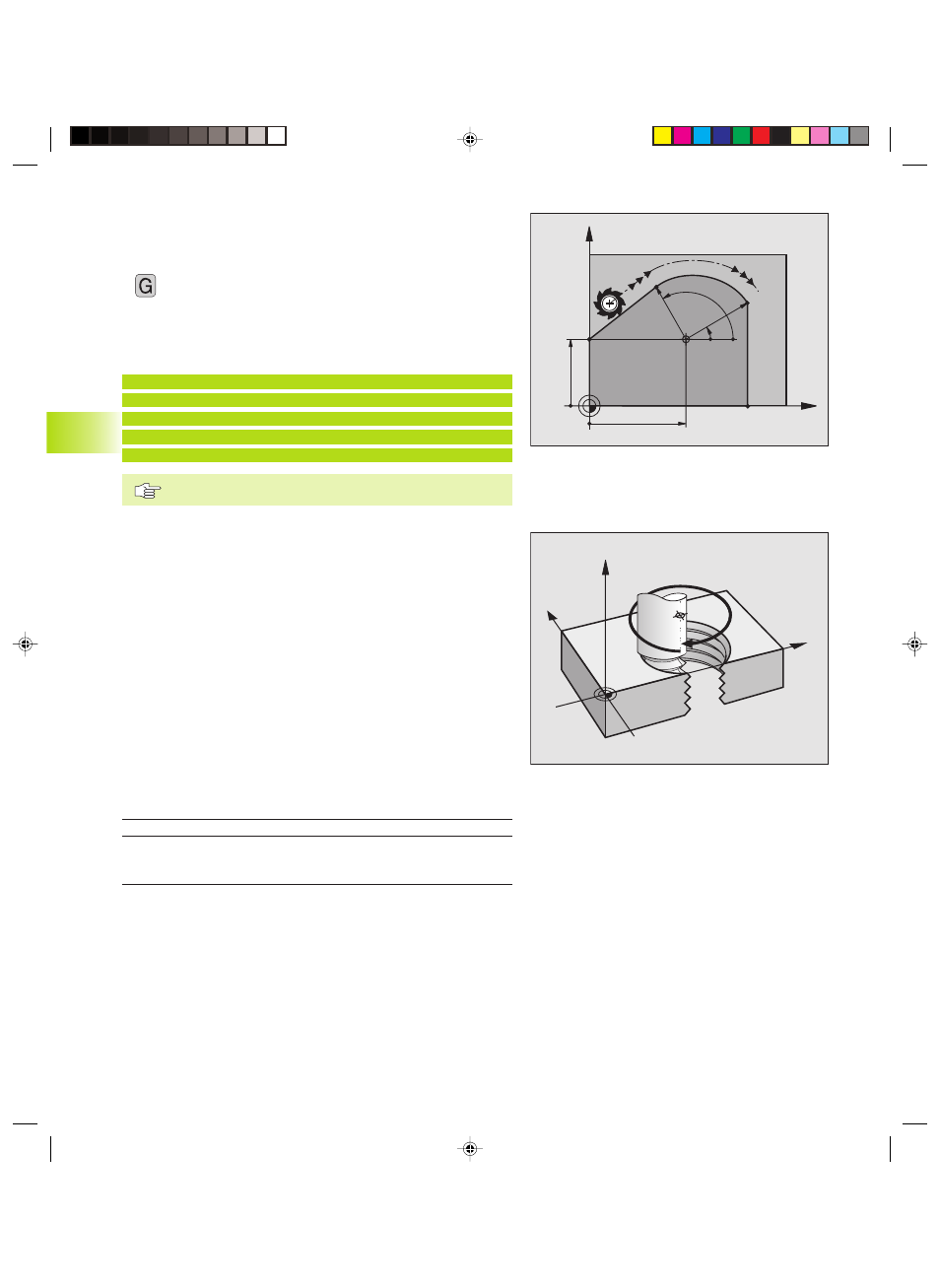
Circular path G16 with tangential approach
The tool moves on a circular path, starting tangentially from a
preceding contour element.
16 ú Polar coordinates radius R: Distance from the arc end
point to the pole I, J
ú Polar coordinates angle H: Angular position of the arc
end point.
Example NC blocks
N120 I+40 J+35 *
N130 G01 G41 X+0 Y+35 F250 M3 *
N140 G11 R+25 H+120 *
N150 G16 R+30 H+30 *
N160 G01 Y+0 *
The pole I, J is not the center of the contour arc!
Helical interpolation
A helix is a combination of a circular movement in a main plane and
a linear movement perpendicular to this plane.
A helix is programmed only in polar coordinates.
Application
■ Large-diameter internal and external threads
■ Lubrication grooves
Calculating the helix
To program a helix, you must enter the total angle through which
the tool is to move on the helix in incremental dimensions, and the
total height of the helix.
For calculating a helix that is to be cut in a upward direction, you
need the following data:
Thread revolutions n Thread revolutions + thread overrun at
the start and end of the thread
Total height h Thread pitch P x thread revolutions n
Incremental Thread revolutions x 360° + angle for
total angle IPA beginning of thread + angle for thread
overrun
Starting coordinate Z Thread pitch P x (thread revolutions +
thread overrun at start of thread)
Gkap6.pm6 29.06.2006, 08:06 114