2 monitor crystals – INFICON XTC/C Thin Film Deposition Controller User Manual
Page 137
5 - 5
IP
N 07
4-
18
3X
XTC/C - XTC/2 Operating Manual
Simple substitutions lead to the equation that was used with the first “frequency
measurement” instruments:
[6]
where the film thickness, T
f
, is proportional (through K) to the frequency
change, DF, and inversely proportional to the density of the film, d
f
. The
constant, K = N
at
d
q
/F
q
2
; where d
q
(= 2.649 gm/cm
3
) is the density of single
crystal quartz and N
at
(=166100 Hz cm) is the frequency constant of AT cut
quartz. A crystal with a starting frequency of 6.0 MHz will display a reduction of
its frequency by 2.27 Hz when 1 angstrom of Aluminum (density of 2.77
gm/cm
3
) is added to its surface. In this manner the thickness of a rigid adlayer
is inferred from the precise measurement of the crystal’s frequency shift. The
quantitative knowledge of this effect provides a means of determining how
much material is being deposited on a substrate in a vacuum system, a
measurement that was not convenient or practical prior to this understanding.
5.5.2 Monitor Crystals
No matter how sophisticated the electronics surrounding it, the essential device
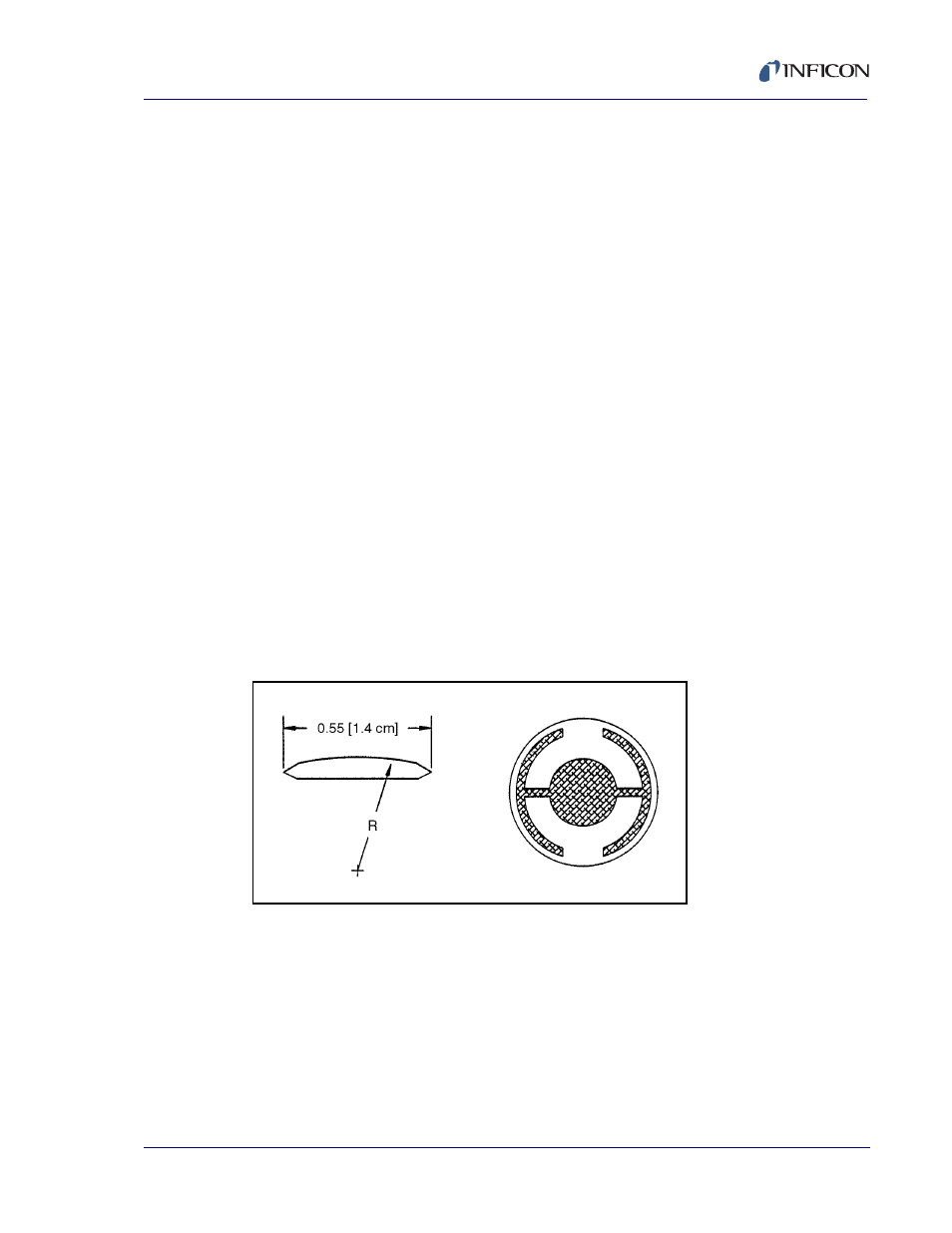
of the deposition monitor is the quartz crystal. The quartz resonator shown in
Figure 5-1
has a frequency response spectrum that is schematically shown in
. The ordinate represents the magnitude of response, or current flow
of the crystal, at the specified frequency.
Figure 5-1 Quartz Resonator
The lowest frequency response is primarily a “thickness shear” mode that is
called the fundamental. The characteristic movement of the thickness shear
mode is for displacement to take place parallel to the major monitor crystal
faces. In other words, the faces are displacement antinodes as shown in
Figure
5-3
. The responses located slightly higher in frequency are called anharmonics;
they are a combination of the thickness shear and thickness twist modes. The
response at about three times the frequency of the fundamental is called the
third quasiharmonic. There are also a series of anharmonics slightly higher in
frequency associated with the quasiharmonic.
T
f
K
F
∆
(
)
d
f
----------------
=
