HP 48gII Graphing Calculator - Manual (Page 776)

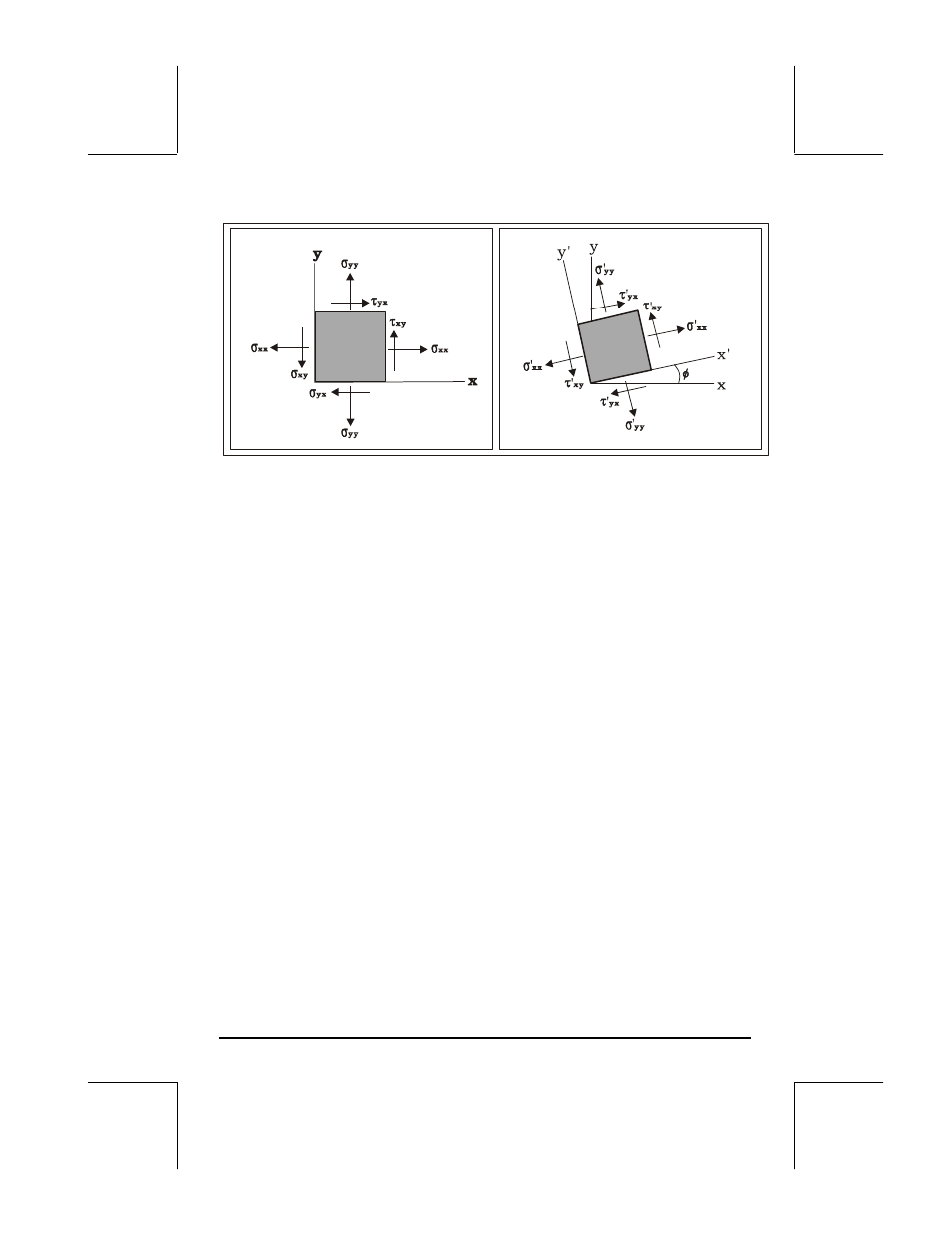
Página 22-36
La relación entre el estado original de tensiones (
σ
xx
, σ
yy
, τ
xy
, τ
yx
) y el estado
de la tensión cuando los ejes se rotan a la izquierda cerca f ( σ’
xx
, σ’
yy
, τ’
xy
,
τ’
yx
), puede ser representado gráficamente por la construcción demostrada en
la figura siguiente.
Para construir el círculo de Mohr utilizamos un sistema coordenado
cartesiano con eje x el corresponder a las tensiones normales (
σ), y eje y el
corresponder a las tensiones de corte ( τ). Localizar los puntos A(σ
xx
, τ
xy
) y
B (σ
yy
, τ
xy
), y dibujar el segmento AB. El punto C donde el segmento AB
cruza el eje σ
n
ser el centro del círculo. Notar que las coordenadas del
punto C son (½ ⋅(σ
yy
+ σ
xy
), 0). Al construir el círculo a mano, usted puede
utilizar un compás para trazar el círculo puesto que usted conoce la
localización del centro C y de dos puntos, A y B.
El segmento AC representa el eje x en el estado original de la tensión. Si
usted desea determinar el estado de la tensión para un sistema de ejes x’-y’,
rotado a la izquierda por un ángulo
φ con respecto al sistema original de ejes
x-y, trace el segmento A’B’, centrado en C y rotado a la derecha cerca y
ángulo
2φ con respecto al segmento AB. Las coordenadas del punto A’
darán los valores ( σ’
xx
, τ’
xy
), mientras que los de B’ dará los valores ( σ’
yy
, τ’
xy
).