HP 48gII Graphing Calculator - Manual (Page 628)

Página 18-40
Ejemplo 2 -- Probar la hipótesis nula H
o
: µ = 22.0 ( = µ
o
), contra la hipótesis
alternativa, H
1
: µ >22.5 en un nivel de confianza de 95% es decir, α = 0.05,
usando una muestra de tamaño n = 25 con una media x = 22.0 y una
desviación estándar s = 3.5. Una vez más, asumimos que no sabemos el
valor de la desviación estándar de la población, por lo tanto, el valor de la
estadística t es al caso de la prueba bilateral demostrado anteriormente, es
decir, t
o
= -0.7142, y el Valor P, para ν = 25 - 1 = 24 grados de libertad es
Valor P = UTPT(24, |-0.7142|) = UTPT(24,0.7124) = 0.2409,
Dado que 0.2409 > 0.05, es decir, Valor P >
α, no podemos rechazar la
hipótesis nula H
o
: µ = 22.0.
Inferencias referentes a dos medias
La hipótesis nula que se probará es H
o
: µ
1
- µ
2
= δ, a un nivel de confianza (1-
α)100%, o nivel de significado α, usar dos muestras de tamaños, n
1
y n
2
,
medias x
1
y x
2
, y desviaciones estándares s
1
y s
2
. Si las desviaciones
estándares de las poblaciones que corresponden a las muestras, σ
1
y σ
2
, se
conocen, o si n
1
> 30 y n
2
> 30 (muestras grandes), la estadística de la
prueba que se utilizará es
2
2
2
1
2
1
2 1
) (
n n
x x
z
o
σ σ
δ
+
− −
=
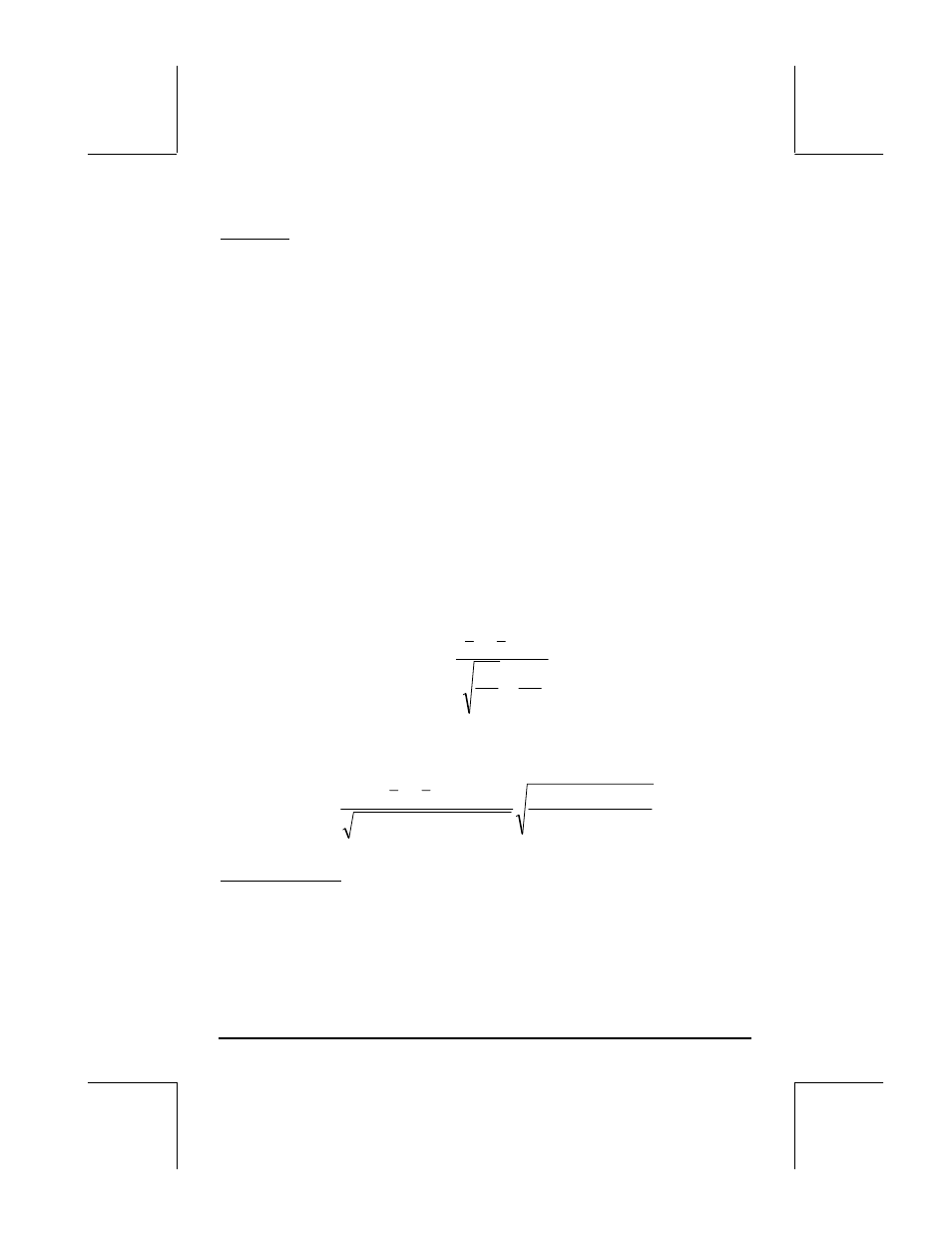
Si n
1
< 30 o n
2
< 30 (por lo menos una muestra pequeña), utilizar la
estadística siguiente de la prueba:
2 1
2 1 2 1
2
2 2
2
1 1
2 1
) 2 (
) 1 ( ) 1 (
) (
n n
n n n n
s n s n
x x
t
+
− +
− + −
− −
=
δ
Hipótesis bilateral
Si la hipótesis alternativa es una hipótesis bilateral, es decir, H
1
: µ
1
- µ
2
≠ δ, el
Valor P para esta prueba se calcula como
•
Si se usa z, Valor P = 2 ⋅UTPN(0,1, |z
o
|)