El menu calc/diff, Solucion de las ecuaciones lineales y no lineales, El menú calc/diff – HP 48gII Graphing Calculator User Manual
Page 499: Solución de las ecuaciones lineales y no lineales
Página 16-4
herramientas útiles para visualizar las curvas y = g(x) que corresponden a
ecuaciones difíciles de resolver analíticamente.
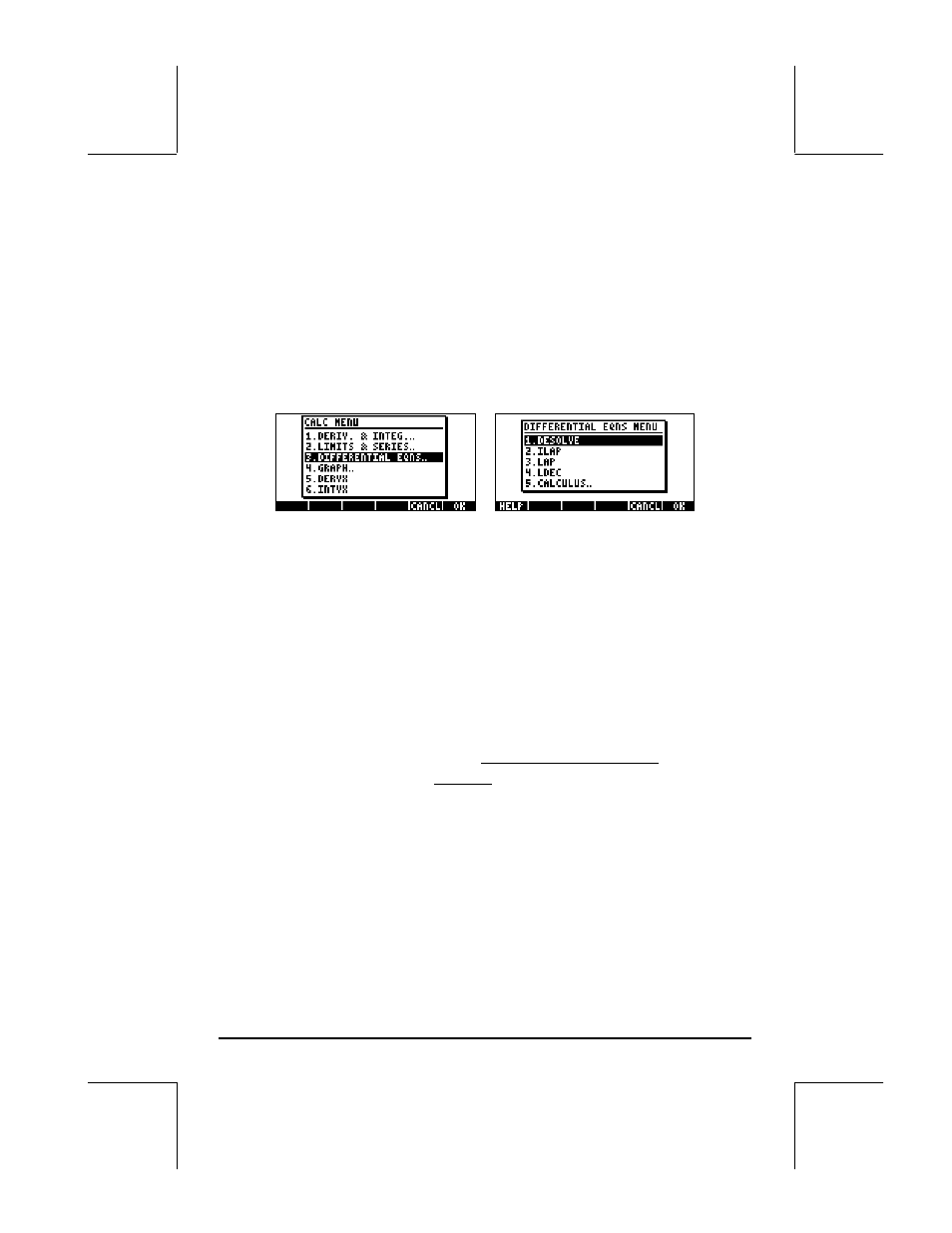
El menú CALC/DIFF
El sub-menú DIFFERENTIAL EQNS.. dentro del menú CALC (
„Ö) provee
funciones para la solución de las ecuaciones diferenciales. El menú
CALC/DIFF que resulta cuando la opción CHOOSE boxes se selecciona para
la señal de sistema 117 es el siguiente:
Estas funciones se describen brevemente a continuación. Las funciones se
describen en forma detallada más adelante en este Capítulo.
DESOLVE: Función para resolver ecuaciones diferenciales, de ser posible
ILAP: Transformada inversa de Laplace, L
-1
[F(s)] = f(t)
LAP: Transformada de Laplace, L[f(t)]=F(s)
LDEC: Función para resolver ecuaciones diferenciales lineales
Solución de las ecuaciones lineales y no lineales
Una ecuación en la cual la variable dependiente y todas sus derivadas son
de primer grado se conoce como una ecuación diferencial lineal. De no ser
así, la ecuación se dice que es no lineal. Ejemplos de ecuaciones
diferenciales lineales son: d
2
x/dt
2
+
β⋅(dx/dt) + ω
o
⋅x = A sin ω
f
t, y
∂C/∂t +
u
⋅(∂C/∂x) = D⋅(∂
2
C/
∂x
2
).
Una ecuación cuyo lado derecho (sin involucrar la función o sus derivadas) es
igual a cero se llama una ecuación homogénea. Si no, se llama no
homogénea. La solución a la ecuación homogénea se conoce como solución
general. Una solución particular es una que satisface la ecuación no
homogénea.
