HP 48gII Graphing Calculator - Manual (Page 519)

Página 16-24
ejemplo, la solución obtenida en el Ejemplo 3 fue y(t) = y
o
cos t + y
1
sin t +
sin(t-3) ⋅H(t-3). Suponga que utilizamos las condiciones iniciales y
o
= 0.5, y y
1
= -0.25. Tracemos esta función para como luce:
• Presione „ô, simultáneamente en modo RPN, para activar la
pantalla PLOT SETUP.
Cambie
TYPE
a
FUNCTION
, de ser necesario
Cambie EQ a ‘0.5*COS(X)-0.25*SIN(X)+SIN(X-3)*H(X-3)’.
Asegúrese que
Indep
se fija a ‘X’.
Presione @ERASE @DRAW para trazar la función.
Presione @EDIT L @LABEL para ver la gráfica.
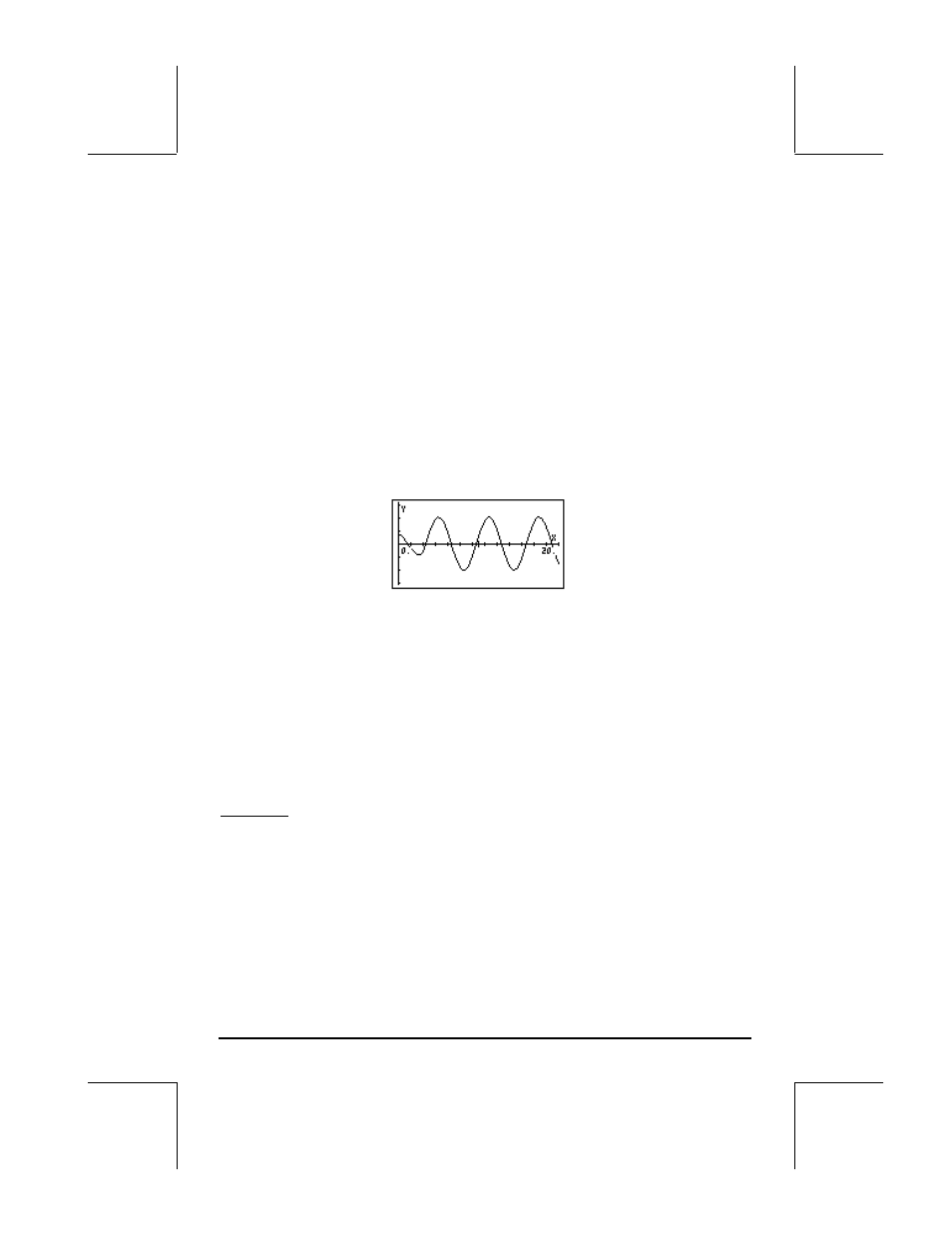
El gráfico que resulta es el siguiente:
Note que la señal comienza con una amplitud relativamente pequeña, pero
repentinamente, en t=3, se cambia a una señal oscilatoria con una amplitud
mayor. La diferencia entre el comportamiento de la señal antes y después t =
3 es el "encendido" de la solución particular y
p
(t) = sin(t-3) ⋅H(t-3). El
comportamiento de la señal antes de que t = 3 represente la contribución de
la solución homogénea, y
h
(t) = y
o
cos t + y
1
sin t.
La solución de una ecuación con una señal de entrada dada por una función
grada de Heaviside se muestra a continuación.
Ejemplo 3 – Determinar la solución a la ecuación, d
2 y/dt 2 +y = H(t-3),
donde H(t) es la función grada de Heaviside. Usando transformadas de
Laplace, podemos escribir: L{d
2 y/dt 2 +y} = L{H(t-3)}, L{d 2 y/dt 2 } + L{y(t)} = L{H(t-
3)}. El término último en esta expresión es: L{H(t-3)} = (1/s) ⋅e –3s . Con Y(s) =
L{y(t)}, y L{d 2 y/dt 2 } = s 2 ⋅Y(s) - s⋅y
o
– y
1
, donde y
o
= h(0) y y
1
= h’(0), la
ecuación transformada es s 2 ⋅Y(s) – s⋅y
o
– y
1
+ Y(s) = (1/s) ⋅e –3s . Cambie el
modo del CAS a Exact, de ser necesario. Use la calculadora para despejar
Y(s), escribiendo: