HP 48gII Graphing Calculator User Manual
Page 371
Página 11-36
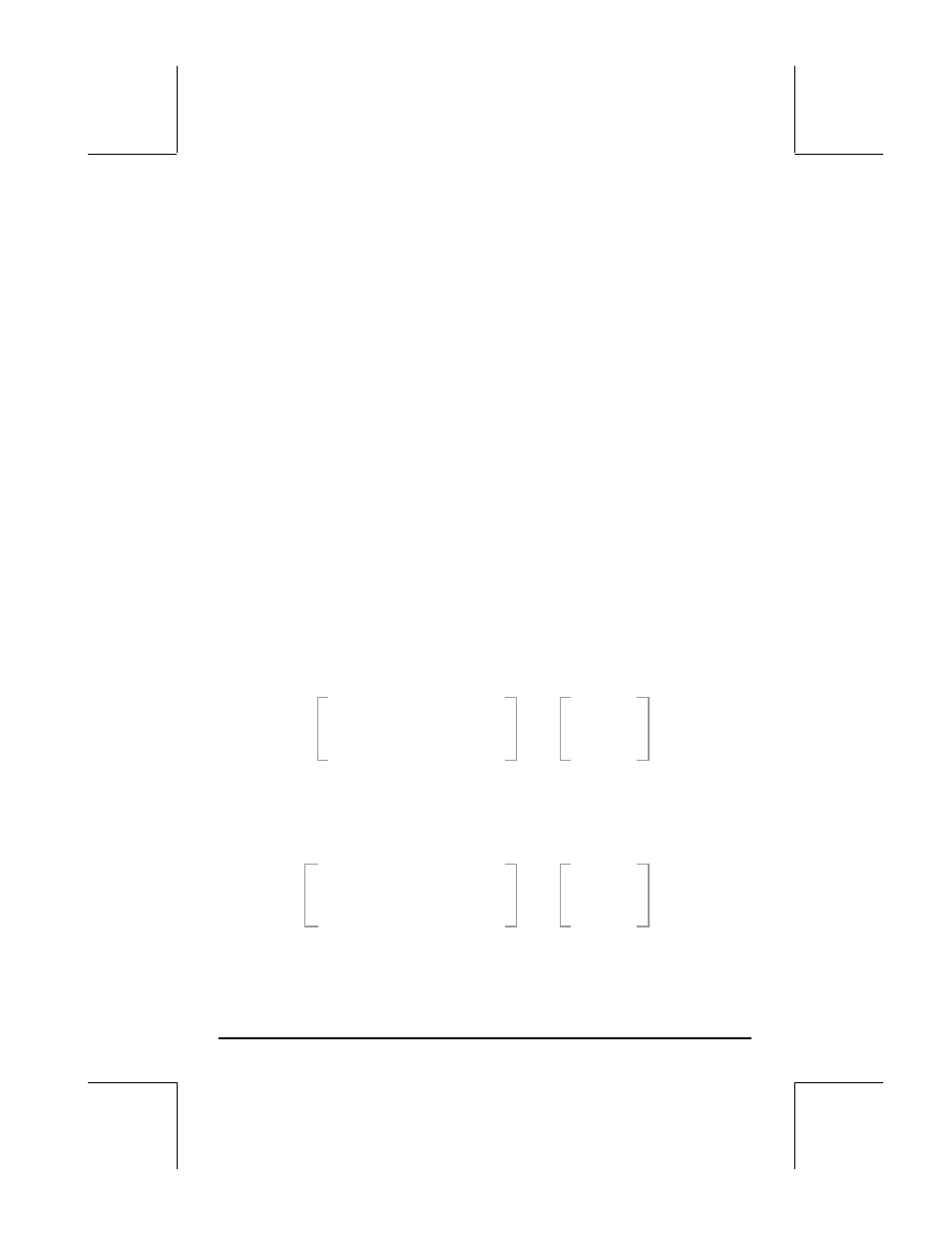
8X +16Y- Z = 41.
La matriz aumentada y la matriz de permutación son las siguientes:
.
1
0
0
0
1
0
0
0
1
,
41
1
16
8
1
3
0
2
2
3
2
1
=
−
−
=
P
A
aug
Almacene la matriz aumentada en la variable AAUG, entonces presione
‚
@AAUG para conseguir una copia en la pantalla. Deseamos mantener la
función CSWP (inglés, Column Swap, o intercambio de columnas) fácilmente
disponible, para lo cual utilizamos:
‚N~~cs~ (encontrar
CSWP), @@OK@@. Usted recibirá un mensaje de error, presione $, e ignore el
mensaje. Después, hacer el menú ROW (inglés, fila) disponible presionando:
„Ø @)CREAT @)@ROW@.
Estamos listos ahora a comenzar la eliminación de Gauss-Jordan con pivoteo
completo. Necesitaremos no perder de vista la matriz de la permutación, así
que anote la matriz
P en papel.
Primero, comprobamos el pivote
a
11
. Notamos que el elemento con el valor
absoluto más grande de la primera fila y de la primera columna es el valor
a
31
= 8. Puesto que quisiéramos que este número fuera el pivote, entonces
intercambiamos las filas 1 y 3, usando:
1#3L @RSWP. La matriz
aumentada y la matriz de permutación son ahora:
8 16 -1
41 0 0 1
2 0
3
-1 0 1 0
1 2
3
2 0 0 1
Comprobando el pivote en la posición (1,1) ahora encontramos que 16 es un
pivote mejor que 8, así, realizamos un intercambio de columnas como sigue:
1#2‚N @@OK@@ @RSWP. La matriz aumentada y la matriz de
permutación son ahora:
16 8
-1
41 0 0 1
0
2
3
-1 1 0 0
2
1
3
2 0 1 0
