HP 48gII Graphing Calculator - Manual (Page 484)

Página 14-7
independientes φ(x
1
, x
2
, …,x
n
), y un vector de las funciones [‘x
1
’ ‘x
2
’…’x
n
’]. La
función HESS produce la matriz Hessiana de la función φ, definida como la
matriz H = [h
ij
] = [ ∂ 2 φ/∂x
i
∂x
j
], el gradiente de la función con respecto a las n-
variables, grad f = [ ∂φ/∂x
1
, ∂φ/∂x
2
, … ∂φ/∂x
n
], y la lista de variables [‘x
1
’
‘x
2
’…’x
n
’].
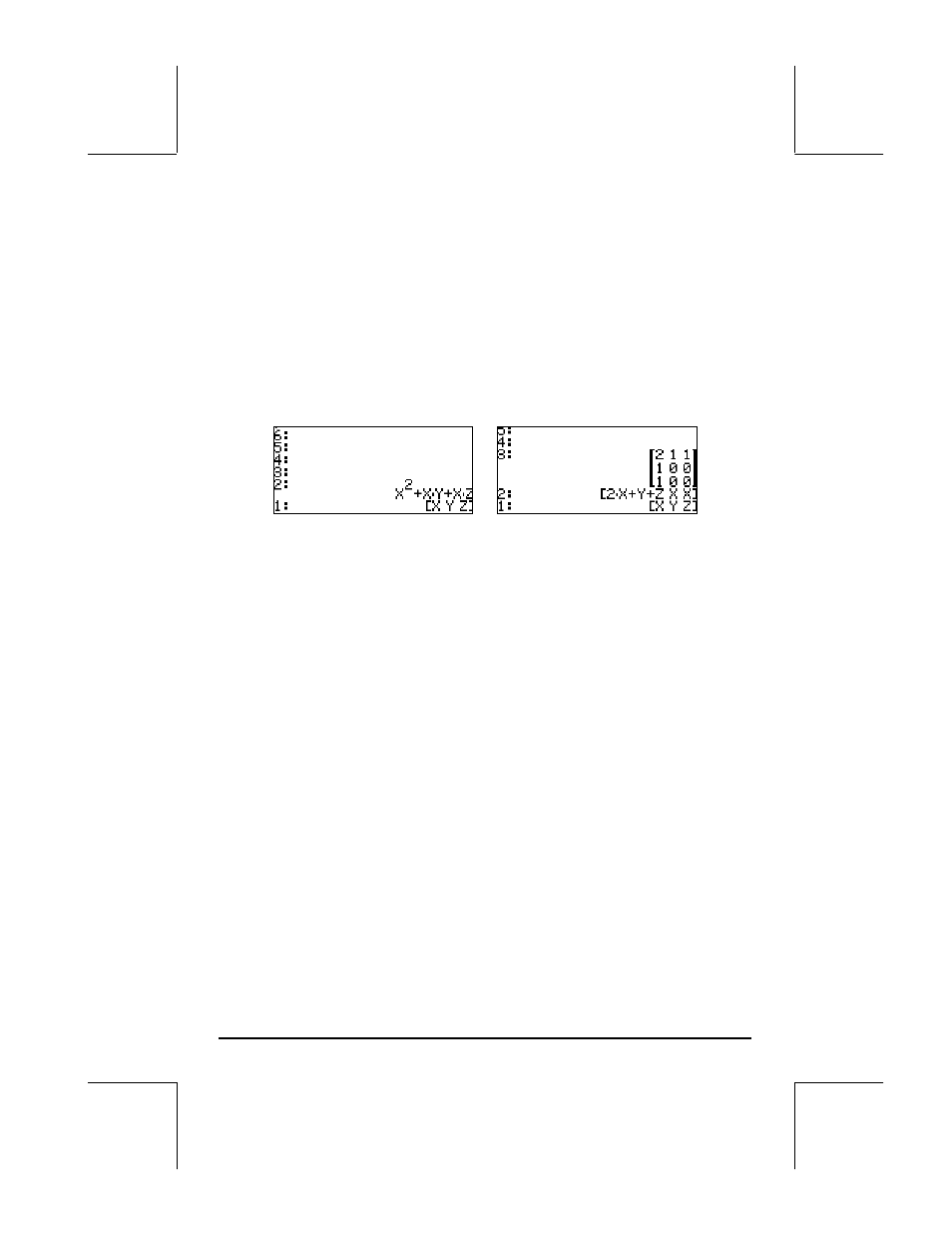
La función HESS es más fácil de visualizar en el modo RPN. Considérese
como ejemplo la función f(X, Y, Z) = X
2 + XY + XZ, aplicaremos la función
HESS a la función φ en el ejemplo siguiente. Las pantallas muestra la pantalla
RPN antes y después de aplicar la función HESS.
Cuando se aplica HESS a una función de dos variables, el gradiente en el
nivel 2, cuando se iguala a cero, representa las ecuaciones para los puntos
críticos, es decir,
∂φ/∂x
i
= 0, mientras que la matriz en el nivel 3 representa
las segundas derivadas. Por lo tanto, los resultados de la función de HESS se
pueden utilizar para analizar extrema en funciones de dos variables. Por
ejemplo, para la función f(X, Y) = X
3 -3X-Y 2 +5, procédase de la forma
siguiente en modo RPN:
‘X^3-3*X-Y^2+5’
` [‘X’,’Y’] ` Escribir función y variables
HESS Aplicar la función HESS
SOLVE Encontrar los puntos críticos
µ Descomponer el vector
‘s1’ K ‘s2’ K Almacenar puntos críticos
Las variables s1 y s2, a este punto, contienen los vectores [ ' X=-1', 'y=0 ] y
[ ' X=1', 'y=0 ], respectivamente. La matriz Hessiana estará en el nivel 1 a
este punto.
‘H’
K Almacenar matriz Hessiana
J @@@H@@@ @@s1@@ SUBST ‚ï Sustituir s1 en H