HP 48gII Graphing Calculator - Manual (Page 522)

Página 16-27
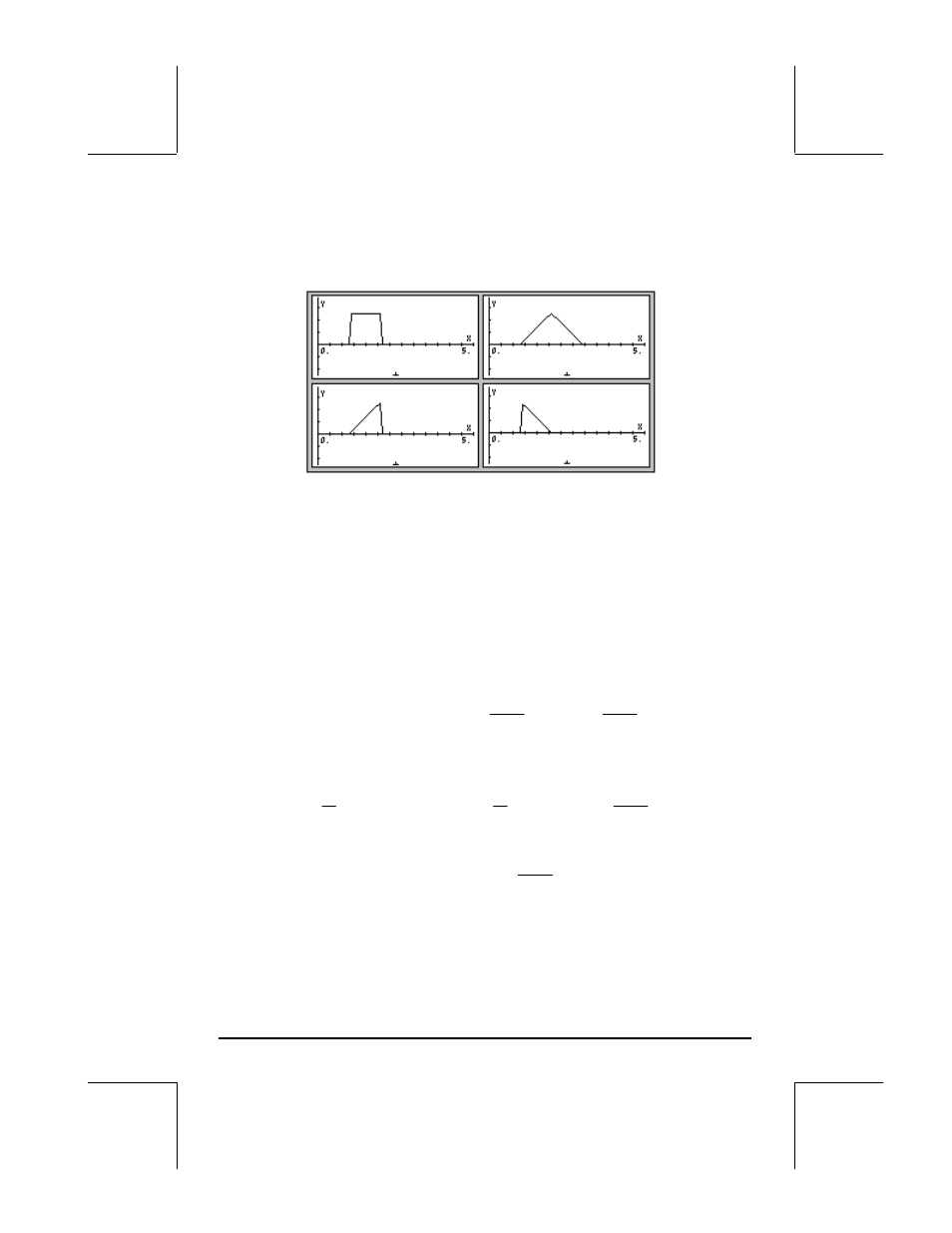
Ejemplos de los diagramas generados por estas funciones, para Uo = 1, a =
2, b = 3, c = 4, rango horizontal = (0,5), y rango vertical = (-1, 1.5), se
demuestran en las figuras siguientes:
Series de Fourier
Las series de Fourier son series que usan las funciones del seno y de coseno
típicamente para ampliar funciones periódicas. Una función f(x) se dice ser
periódica, de período T, si f(x+T) = f(t). Por ejemplo, porque sin(x+2
π) = sin
x, y cos(x+2 π) = cos x, las funciones sin y cos son funciones periódicas de
período 2 π. Si dos funciones f(x) y g(x) son periódico de período T, entonces
su combinación linear h(x) = a ⋅f(x) + b⋅g(x), es también periódica de período
T. Dada una función periódica de período T, f(t), puede ser ampliado en
una serie de funciones del seno y de coseno conocidas como serie de Fourier,
∑
∞
=






⋅ + ⋅ + =
1
0
2
sin
2
cos ) (
n
n n
t
T
n
b t
T
n
a a t f
π π
con a
n
y b
n
calculados por
∫ ∫
− −
⋅ ⋅ = ⋅ =
2 /
2 /
2 /
2 /
0
,
2
cos ) (
2
, ) (
1
T
T
T
T
n
dt t
T
n
t f
T
a dt t f
T
a
π
∫
−
⋅ ⋅ =
2 /
2 /
.
2
sin ) (
T
T
n
dt t
T
n
t f b
π
Los ejercicios siguientes son en modo ALG , con el modo del CAS fijado a
Exact. (Cuando usted produce un gráfico, el modo del CAS será reajustado