HP 48gII Graphing Calculator - Manual (Page 384)

Página 11-49
En resumen,
λ
1
= 0.29, x
1
= [ 1.00,0.79,–0.91] T ,
λ
2
= 3.16, x
2
= [1.00,-0.51, 0.65] T ,
λ
3
= 7.54, x
1
= [-0.03, 1.00, 0.84] T .
Nota: Una matriz simétrica tiene valores propios reales solamente, y sus
vectores propios son mutuamente perpendiculares. Para comprobar esto en el
ejemplo apenas resuelto, calcule
x
1
• x
2
= 0, x
1
• x
3
= 0, y x
2
• x
3
= 0.
Función JORDAN
La función JORDAN se usa para producir la diagonalización o
descomposición de ciclo de Jordan de una matriz. En modo RPN, dada una
matriz cuadrada
A, la función JORDAN produce cuatro salidas, a saber:
• El polinomio del mínimo de la matriz A (nivel 4)
• El polinomio característico de la matriz A (nivel 3)
• Una lista con los vectores propios que corresponden a cada valor
propio de la matriz A (nivel 2)
• Un vector con los vectores propios de la matriz A (nivel 1)
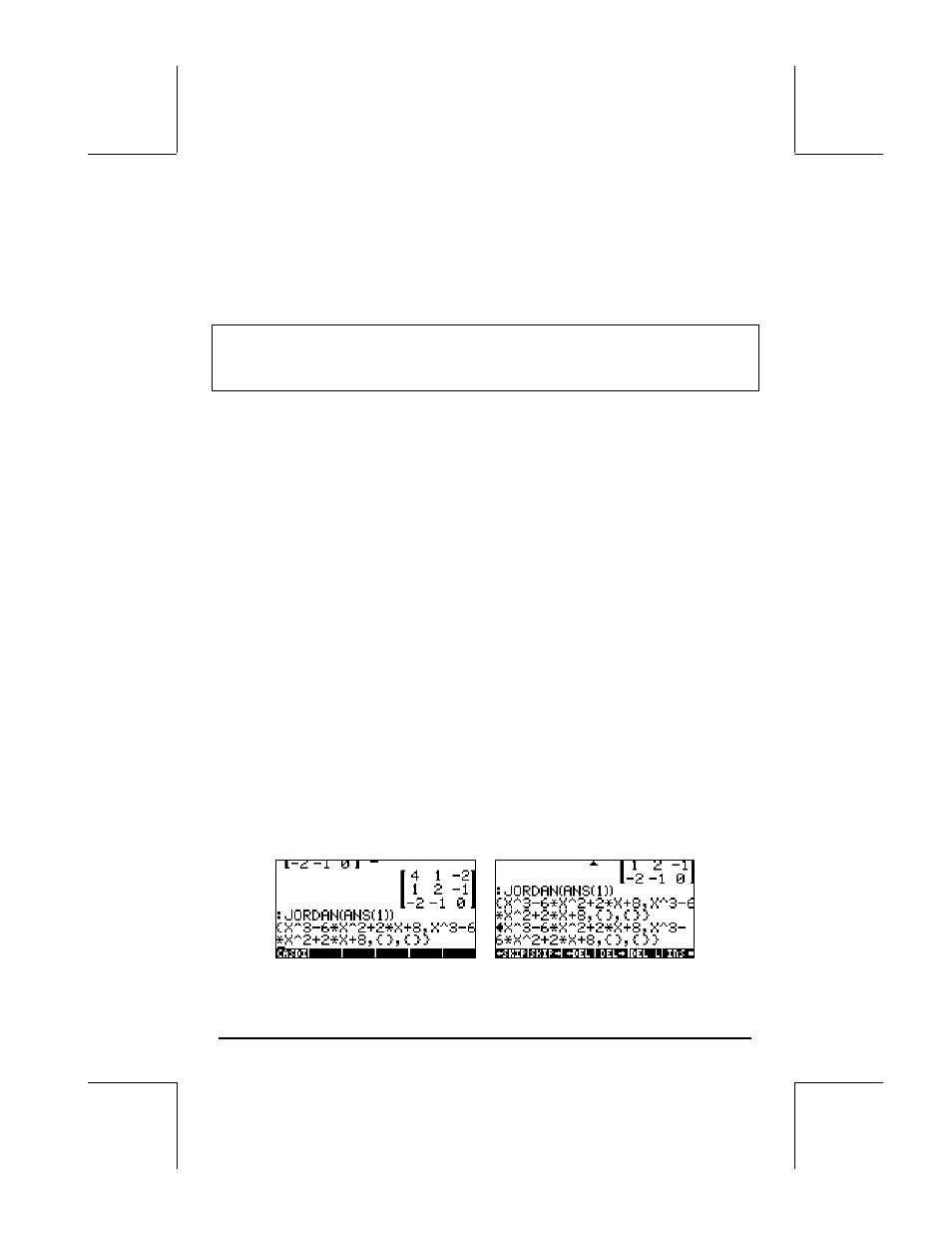
Por ejemplo, intente este ejercicio en modo RPN:
[[4,1,-2],[1,2,-1],[-2,-1,0]] JORDAN
La salida es la siguiente:
4: ‘X^3+-6*x^2+2*X+8’
3: ‘X^3+-6*x^2+2*X+8’
2: { }
1: { }
El mismo ejercicio, en modo ALG, se muestra en la siguientes pantallas: