Caracteristicas de la transformada de fourier – HP 48gII Graphing Calculator User Manual
Page 543
Página 16-48
Notas:
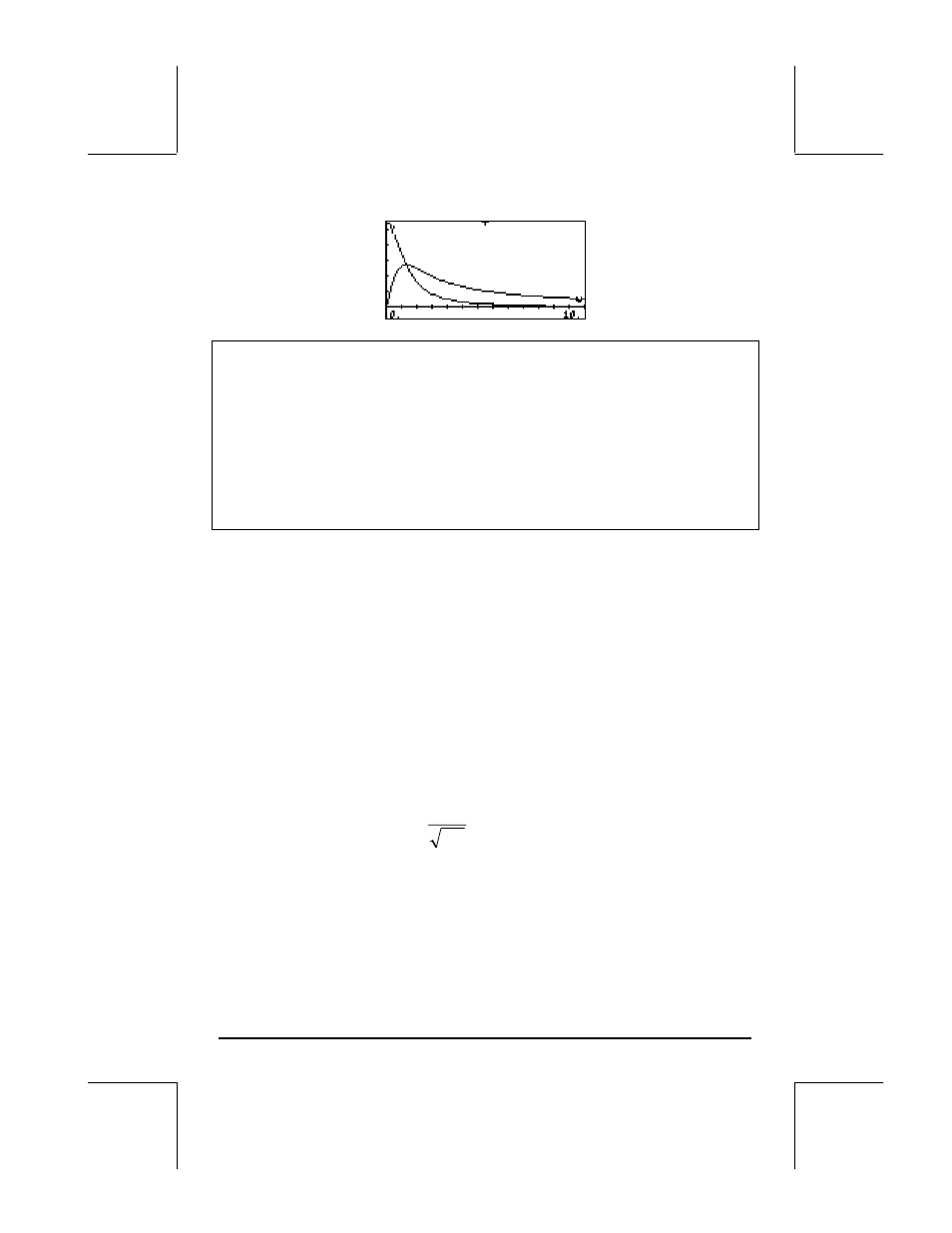
La magnitud, o valor absoluto, de la transformada de Fourier, |F(
ω)|, es el
espectro de la frecuencia de la función original f(t). Por el ejemplo
demostrado anteriormente, |F(
ω)| = 1/[2π(1+ω
2
)]
1/2
. El diagrama de |F(
ω)|
vs.
ω se mostró anteriormente.
Algunas funciones, tales como valores constantes, sin x, exp(x), x
2
, etc., no
tienen transformada de Fourier. Las funciones que van a cero suficientemente
rápido cuando x va al infinito tienen transformadas de Fourier.
Características de la transformada de Fourier
Linealidad: Si a y b son constantes, y f y g funciones, entonces F{a
⋅f + b⋅g} =
a F{f }+ b F{g}.
Transformación de derivadas parciales. Sea u = u(x,t). Si la transformada de
Fourier transforma la variable x, entonces
F{
∂u/∂x} = iω F{u},
F{
∂
2
u/
∂x
2
} = -
ω
2
F{u},
F{
∂u/∂t} = ∂F{u}/∂t, F{∂
2
u/
∂t
2
} =
∂
2
F{u}/
∂t
2
Convolución: Para aplicaciones de la transformada de Fourier, la operación
de convolución se define como
∫
⋅
⋅
−
⋅
=
.
)
(
)
(
2
1
)
)(
*
(
ξ
ξ
ξ
π
d
g
x
f
x
g
f
Las siguientes características aplican para la convolución:
F{f*g} = F{f}
⋅F{g}.
