HP 48gII Graphing Calculator User Manual
Page 627
Página 18-39
desviación de estándar s = 3.5. Asumimos que no sabemos el valor de la
desviación de estándar de la población, por lo tanto, calculamos una
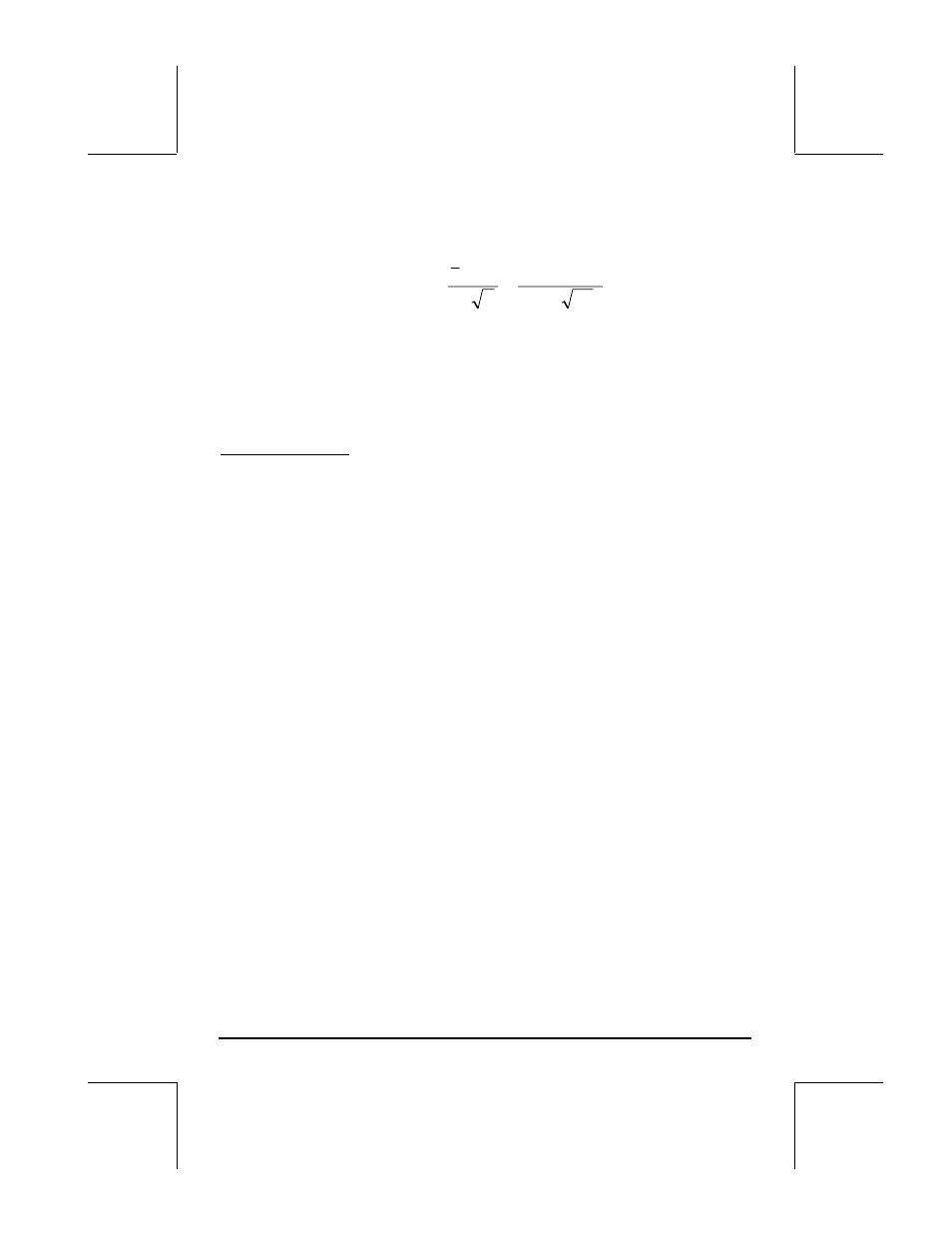
estadística de t como sigue:
7142
.
0
25
/
5
.
3
5
.
22
0
.
22
/
−
=
−
=
−
=
n
s
x
t
o
o
µ
El correspondiente Valor P, para n = 25 - 1 = 24 grados de libertad es
Valor P = 2
⋅UTPT(24,-0.7142) = 2⋅0.7590 = 1.5169,
dado que 1.5169 > 0.05, es decir, Valor P >
α, no podemos rechazar la
hipótesis nula H
o
:
µ = 22.0.
Hipótesis unilateral
El problema consiste en la prueba de la hipótesis nula H
o
:
µ = µ
o
, contra la
hipótesis alternativa, H
1
:
µ > µ
ο
ó H
1
:
µ < µ
ο
a un nivel de confianza de (1-
α)100%, o a un nivel de significado α, usando una muestra de tamaño n con
una media
x y una desviación estándar s. Esta prueba se refiere como
prueba unilateral (o de una cola). El procedimiento para realizar una prueba
unilateral comienza como en la prueba bilateral calculando la estadística
apropiada para la prueba (t
o
o z
o
) como se indicó anteriormente.
A continuació, se usa el Valor P asociado con z
ο
ó t
ο
, y se compara con
α
para decidir si o no rechazar la hipótesis nula. El Valor P para una prueba
bilateral se define como
Valor P = P(z > |z
o
|), ó, Valor P = P(t > |t
o
|).
Los criterios a utilizar para la prueba de la hipótesis son:
•
Rechazar H
o
si Valor P <
α
•
No rechaza H
o
si Valor P >
α.
Notar que los criterios están exactamente iguales que en la prueba bilateral.
La diferencia principal es la manera como el Valor P se calcula. El Valor P
para una prueba unilateral puede ser calculado usando las funciones de la
probabilidad en la calculadora como sigue:
•
Si se usa z,
Valor P = UTPN(0,1,z
o
)
•
Si se usa t,
Valor P = UTPT(
ν,t
o
)
