HP 48gII Graphing Calculator - Manual (Page 514)

Página 16-19
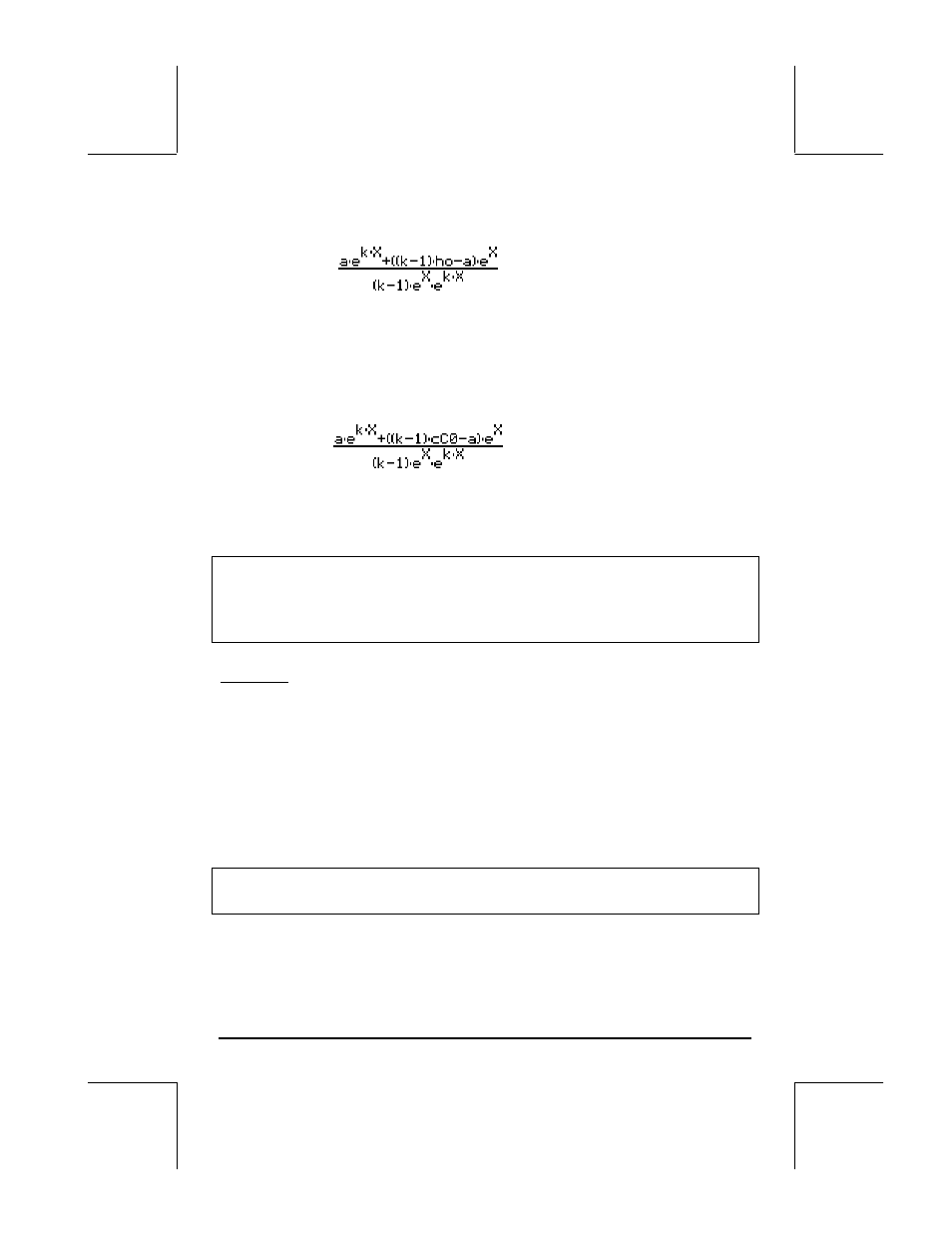
El resultado es . Substituyendo X por t en esta
expresión y simplificándolo, resulta en h(t) = a/(k-1) ⋅e -t +((k-1) ⋅h
o
-a)/(k-1) ⋅e -kt .
Comprobar lo que la solución a la EDO ser si usted utiliza la función LDEC:
‘a*EXP(-X)’ ` ‘X+k’ ` LDEC µ
El resultado es: , es decir,
h(t) = a/(k-1) ⋅e -t +((k-1) ⋅cC
o
-a)/(k-1) ⋅e -kt .
Por lo tanto, cC0 en los resultados de LDEC representa la condición inicial
h(0).
Nota: Al usar la función LDEC para solucionar un EDO lineal de orden n en
f(X), el resultado será dado en términos de las n constantes cC0, cC1,
cC2, …, cC(n-1), representando las condiciones iniciales f(0), f’(0), f”(0), …,
f
(n-1) (0).
Ejemplo 2 – Use Transformadas de Laplace para solucionar la ecuación lineal
de segundo orden,
d 2 y/dt 2 +2y = sin 3t.
Usando Transformadas de Laplace, podemos escribir:
L{d 2 y/dt 2 +2y} = L{sin 3t},
L{d 2 y/dt 2 } + 2 ⋅L{y(t)} = L{sin 3t}.
Nota: ‘SIN(3*X)’ ` LAP µ produce ‘3/(X^2+9)’, es decir,
L{sin 3t}=3/(s 2 +9).