HP 48gII Graphing Calculator - Manual (Page 348)

Página 11-13
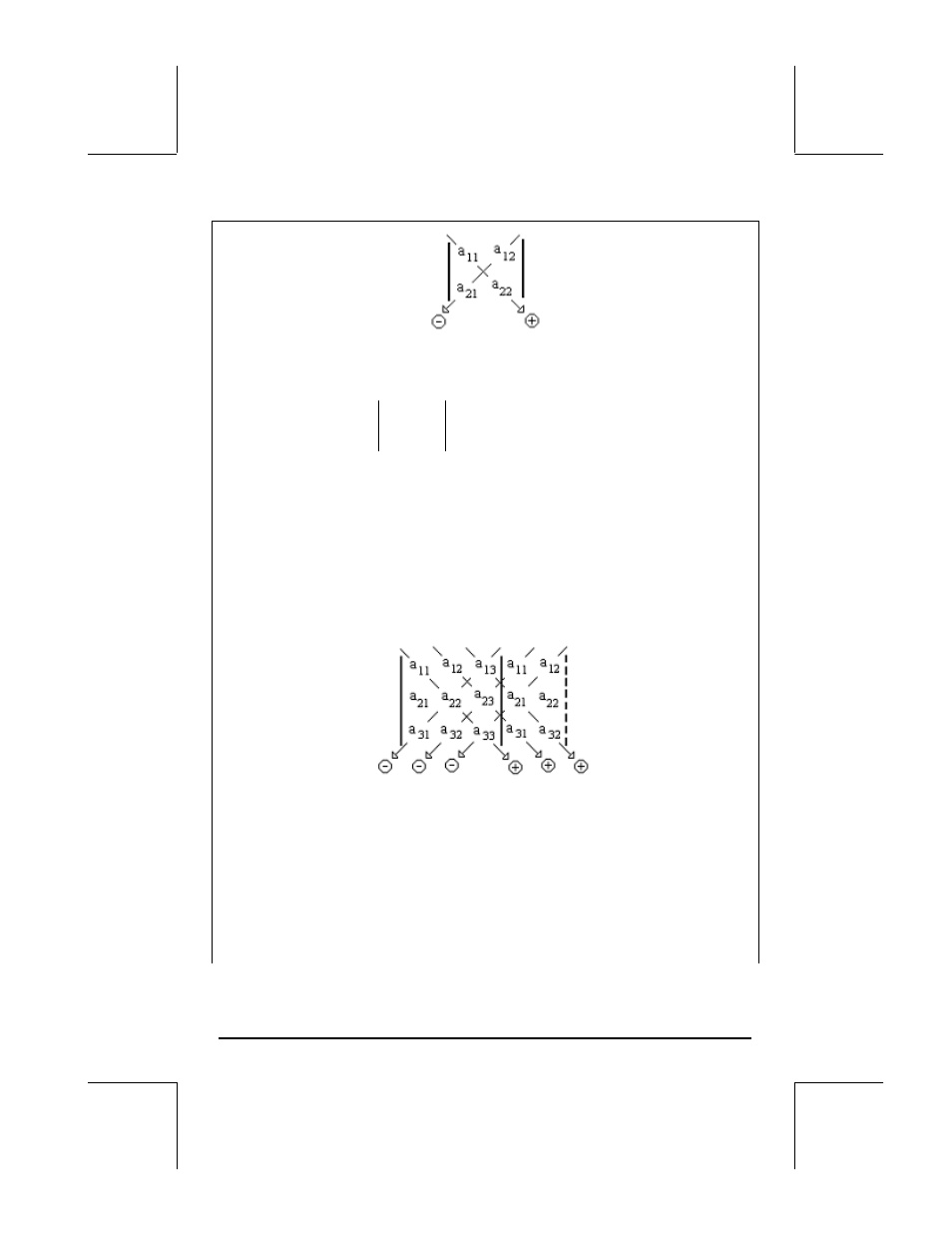
El determinante 2
×2 es, por lo tanto,
21 12 22 11
22 21
12 11 a a a a
a a
a a
⋅ − ⋅ =
Un determinante 3
×3 es calculado aumentando el determinante, una
operación que consista en copiar las primeras dos columnas del
determinante, y colocarlas a la derecha de la columna 3, según lo
demostrado en el diagrama siguiente. El diagrama también muestra los
elementos que se multiplicarán con el signo correspondiente adjunto al
producto, de manera similar a lo hecho anteriormente para un determinante
2
×2. Después de la multiplicación los resultados se agregan para obtener el
determinante.
Para las matrices cuadradas de una orden mayor, los determinantes pueden
ser calculados usando determinantes de una orden menor, llamados
cofactores. La idea general es "ampliar" el determinante de una matriz n
×n
(también designado un determinante n ×n) en una suma de los cofactores, que
son los determinantes (n-1) ×(n-1), multiplicado por los elementos de una sola
fila o columna, con signos positivos y negativos alternados. . Esta
"extensión" entonces se lleva al nivel (más bajo) siguiente, con los cofactores
de orden (n-2)
×(n-2), y así sucesivamente, hasta terminar solamente con una