HEIDENHAIN TNC 320 (340 551-01) - Manual (Page 138)

138 –˜pV"hhamV9˜pV"hhamV˜ pm›p¤’
6.5 P
a
th Cont
ours—P
olar Coor
dinat
e
s
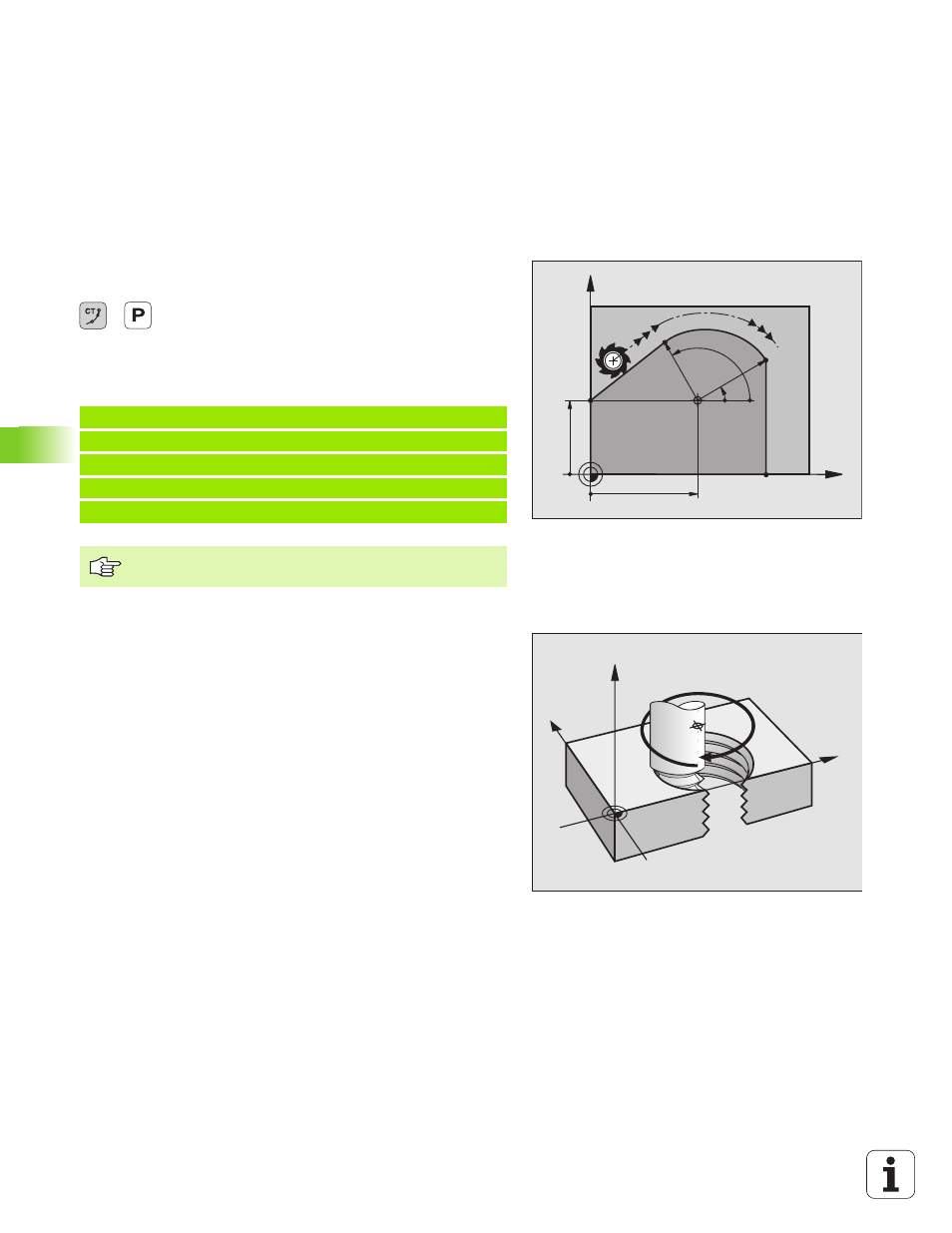
Circular Path CTP with Tangential Connection
^F˜›ppd˜hp¦F’˜pm˜"˜4a4¤d"˜z"›^:˜’›"›amV˜›"mVFm›a"dd©˜Oph˜"˜
zF4F=amV˜4pm›p¤˜FdFhFm›
8 Polar coordinates radius PR: ˜ a’›"m4F˜Oph˜›^F˜"4˜
Fm=˜zpam›˜›p˜›^F˜zpdF˜
8 Polar coordinates angle PA:
˜ mV¤d"˜zp’a›apm˜pO˜›^F˜
"4˜Fm=˜zpam›
Example NC blocks
Helical interpolation
˜^Fda¨˜a’˜"˜4ph*am"›apm˜pO˜"˜4a4¤d"˜hp¦FhFm›˜am˜"˜h"am˜zd"mF˜"m=˜"˜
damF"˜hp¦FhFm›˜zFzFm=a4¤d"˜›p˜›^a’˜zd"mF
˜^Fda¨˜a’˜zpV"hhF=˜pmd©˜am˜zpd"˜4pp=am"›F’
Application
„ "VF_=a"hF›F˜am›Fm"d˜"m=˜F¨›Fm"d˜›^F"=’
„ ¤*a4"›apm˜Vpp¦F’
Calculating the helix
p˜zpV"h˜"˜^Fda¨:˜©p¤˜h¤’›˜Fm›F˜›^F˜›p›"d˜"mVdF˜›^p¤V^˜§^a4^˜›^F˜
›ppd˜a’˜›p˜hp¦F˜pm˜›^F˜^Fda¨˜am˜am4FhFm›"d˜=ahFm’apm’:˜"m=˜›^F˜›p›"d˜
^FaV^›˜pO˜›^F˜^Fda¨
p˜4"d4¤d"›amV˜"˜^Fda¨˜›^"›˜a’˜›p˜*F˜4¤›˜am˜"m˜¤z§"=˜=aF4›apm:˜©p¤˜mFF=˜
›^F˜Opddp§amV˜="›"9
12 CC X+40 Y+35
13 L X+0 Y+35 RL F250 M3
14 LP PR+25 PA+120
15 CTP PR+30 PA+30
16 L Y+0
^F˜zpdF˜ ˜a’˜not˜›^F˜4Fm›F˜pO˜›^F˜4pm›p¤˜"4M
X
Y
40
35
CC
30°
120°
R30 R25
^F"=˜F¦pd¤›apm’˜m ^F"=˜F¦pd¤›apm’˜‚˜›^F"=˜p¦F¤m˜"›˜
›^F"=˜*FVammamV˜"m=˜Fm=
p›"d˜^FaV^›˜^ ^F"=˜za›4^˜˜›ahF’˜›^F"=˜F¦pd¤›apm’˜m
m4FhFm›"d˜›p›"d˜
"mVdF˜
¤h*F˜pO˜F¦pd¤›apm’˜›ahF’˜–¬@˜‚˜"mVdF˜Op˜
*FVammamV˜pO˜›^F"=˜‚˜"mVdF˜Op˜›^F"=˜
p¦F¤m
›"›amV˜4pp=am"›F˜! a›4^˜˜›ahF’˜|›^F"=˜F¦pd¤›apm’˜‚˜›^F"=˜
p¦F¤m˜"›˜’›"›˜pO˜›^F"=}
Y
X
Z
CC