Casio ClassPad II fx-CP400 - Manual (Page 68)

Chapter 2: Main Application 68
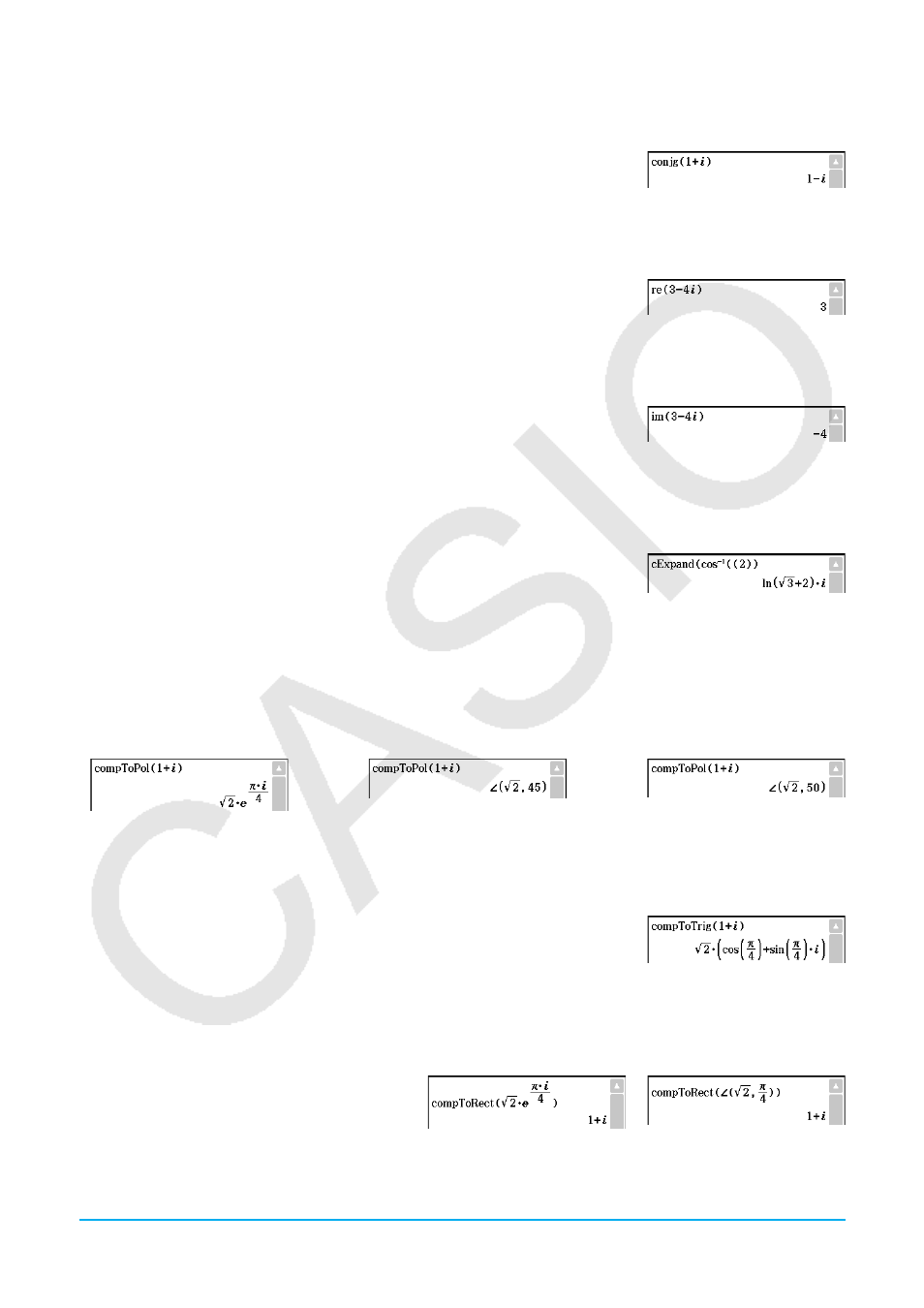
u conjg [Action][Complex][conjg]
Function: Returns the conjugate complex number.
Syntax: conjg (Exp/Eq/Ineq /List/Mat [ ) ] (Ineq : Real mode only)
Example: To obtain the conjugate of complex number 1 + i
u re [Action][Complex][re]
Function: Returns the real part of a complex number.
Syntax: re (Exp/Eq/Ineq /List/Mat [ ) ] (Ineq : Real mode only)
Example: To obtain the real part of complex number 3 – 4 i
u im [Action][Complex][im]
Function: Returns the imaginary part of a complex number.
Syntax: im (Exp/Eq/Ineq /List/Mat [ ) ] (Ineq : Real mode only)
Example: To obtain the imaginary part of complex number 3 – 4 i
u cExpand [Action][Complex][cExpand]
Function: Expands a complex expression to rectangular form (a + b i ).
Syntax: cExpand (Exp/Eq/List/Mat [ ) ]
• The variables are regarded as real numbers.
Example: To expand cos –1 (2) (in the Radian mode)
u compToPol [Action][Complex][compToPol]
Function: Transforms a complex number into its polar form.
Syntax: compToPol (Exp/Eq/List/Mat [ ) ]
• When the argument is Mat (Matrices), calculation can be performed using the Radian angle unit only.
Example: To transform 1 + i into its polar form
Radian mode Degree mode Grad mode
u compToTrig [Action][Complex][compToTrig]
Function: Transforms a complex number into its trigonometric/hyperbolic form.
Syntax: compToTrig (Exp/Eq/List/Mat [ ) ]
Example: To transform 1 + i into its trigonometric form (in the Radian mode)
u compToRect [Action][Complex][compToRect]
Function: Transforms a complex number into its rectangular form.
Syntax: compToRect (
Є( r , Ƨ ) or r · e^( Ƨ · i ) form [ ) ]
Example: To transform a complex number
into its rectangular form