Casio ClassPad II fx-CP400 User Manual
Page 63
Chapter 2: Main Application
63
Syntax:
laplace(
f
(
t
),
t
,
s
)
f
(
t
): expression ;
t
: variable with respect to which the expression is
transformed ;
s
: parameter of the transform
invLaplace(
L
(
s
),
s
,
t
)
L
(
s
): expression ;
s
: variable with respect to which the expression is
transformed ;
t
: parameter of the transform
ClassPad supports transform of the following functions.
sin(
x
), cos(
x
), sinh(
x
), cosh(
x
),
x
n
,
'
x
,
e
x
, heaviside(
x
), delta(
x
), delta(
x
,
n
)
ClassPad does not support transform of the following functions.
tan(
x
), sin
– 1
(
x
), cos
– 1
(
x
), tan
– 1
(
x
), tanh(
x
), sinh
– 1
(
x
), cosh
– 1
(
x
), tanh
– 1
(
x
), log(
x
), ln(
x
), 1/
x
, abs(
x
), gamma(
x
)
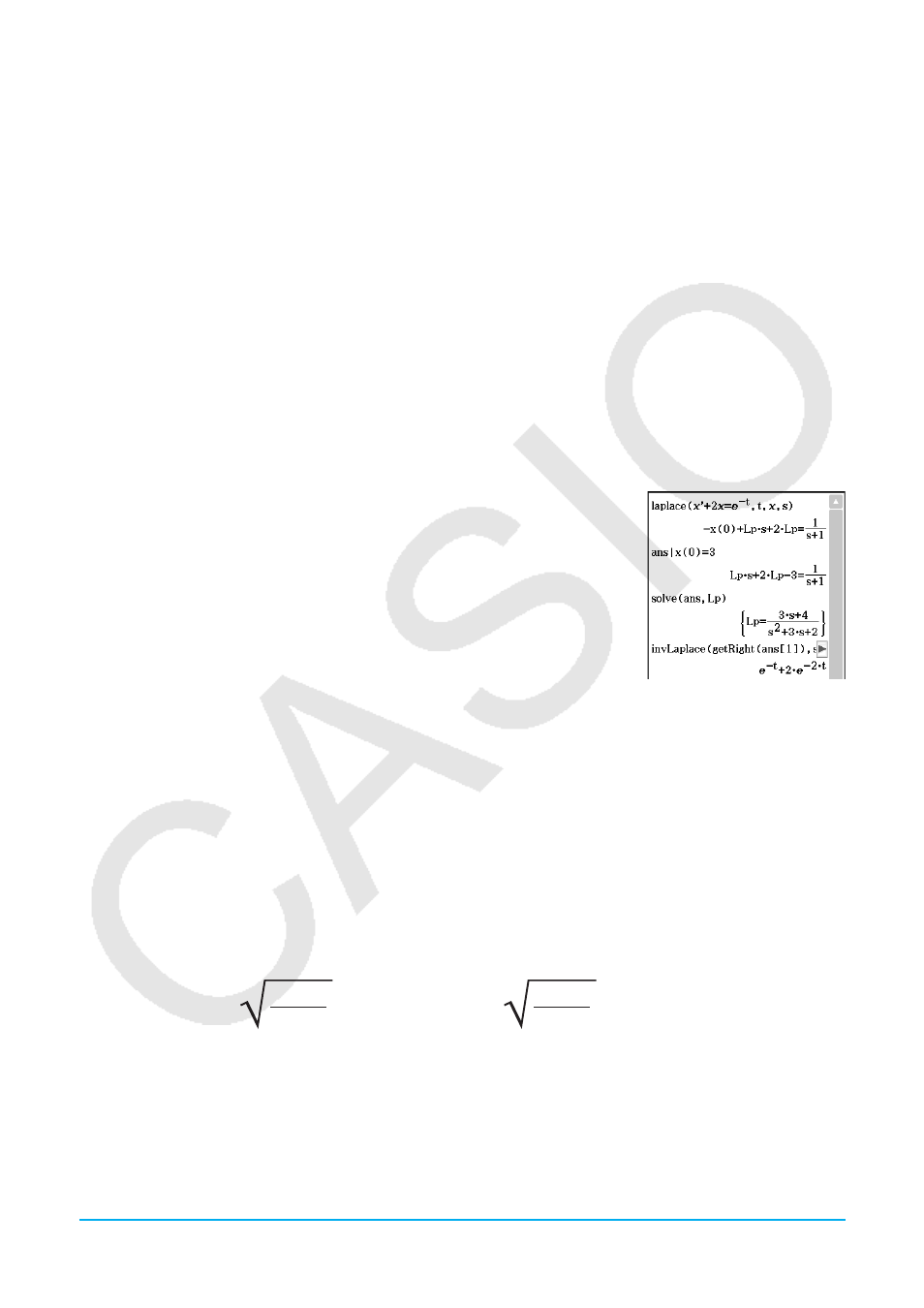
Laplace Transform of a Differential Equation
The laplace command can be used to solve ordinary differential equations. ClassPad does not support System
of Differential Equations for laplace.
Syntax: laplace(diff eq,
x
,
y
,
t
)
diff eq: differential equation to solve ;
x
: independent variable in the diff eq ;
y
: dependent variable in the diff eq ;
t
: parameter of the transform
Example: To solve a differential equation
x
’ + 2
x
=
e
−
t
where
x
(0) = 3 using the
Laplace transform
Lp means
F
(
s
) =
L
[
f
(
t
)] in the result of transform for a differential equation.
u fourier [Action][Advanced][fourier], invFourier [Action][Advanced][invFourier]
Function: “fourier” is the command for the Fourier Transform, and “invFourier” is the command for the inverse
Fourier Transform.
Syntax: fourier(
f
(
x
),
x
,
w
,
n
) invFourier(
f
(
w
),
w
,
x
,
n
)
x
: variable with respect to which the expression is transformed with ;
w
: parameter of the transform ;
n
: 0 to 4, indicating Fourier parameter to use (optional)
ClassPad supports transform of the following functions.
sin(
t
), cos(
t
), log(
t
), ln(
t
), abs(
t
), signum(
t
), heaviside(
t
), delta(
t
), delta(
t
,
n
),
e
ti
ClassPad does not support transform of the following functions.
tan(
t
), sin
– 1
(
t
), cos
– 1
(
t
), tan
– 1
(
t
), sinh(
t
), cosh(
t
), tanh(
t
), sinh
– 1
(
t
), cosh
– 1
(
t
), tanh
– 1
(
t
), gamma(
t
),
'
t
,
e
t
The Fourier Transform pairs are defined using two arbitrary constants
a
,
b
.
∫
∞
–
∞
I
(
W
)
H
LE
ωW
GW
)
(
ω
)
=
⏐
E
⏐
(2
π
)
1–D
∫
∞
–
∞
)
(
ω
)
H
–
LE
ωW
G
ω
I
(
W
)
=
⏐
E
⏐
(2
π
)
1+D
The values of
a
and
b
depend on the scientific discipline, which can be specified by the value of
n
(optional
fourth parameter of fourier and invFourier) as shown below.
