Altera Floating-Point User Manual
Page 28
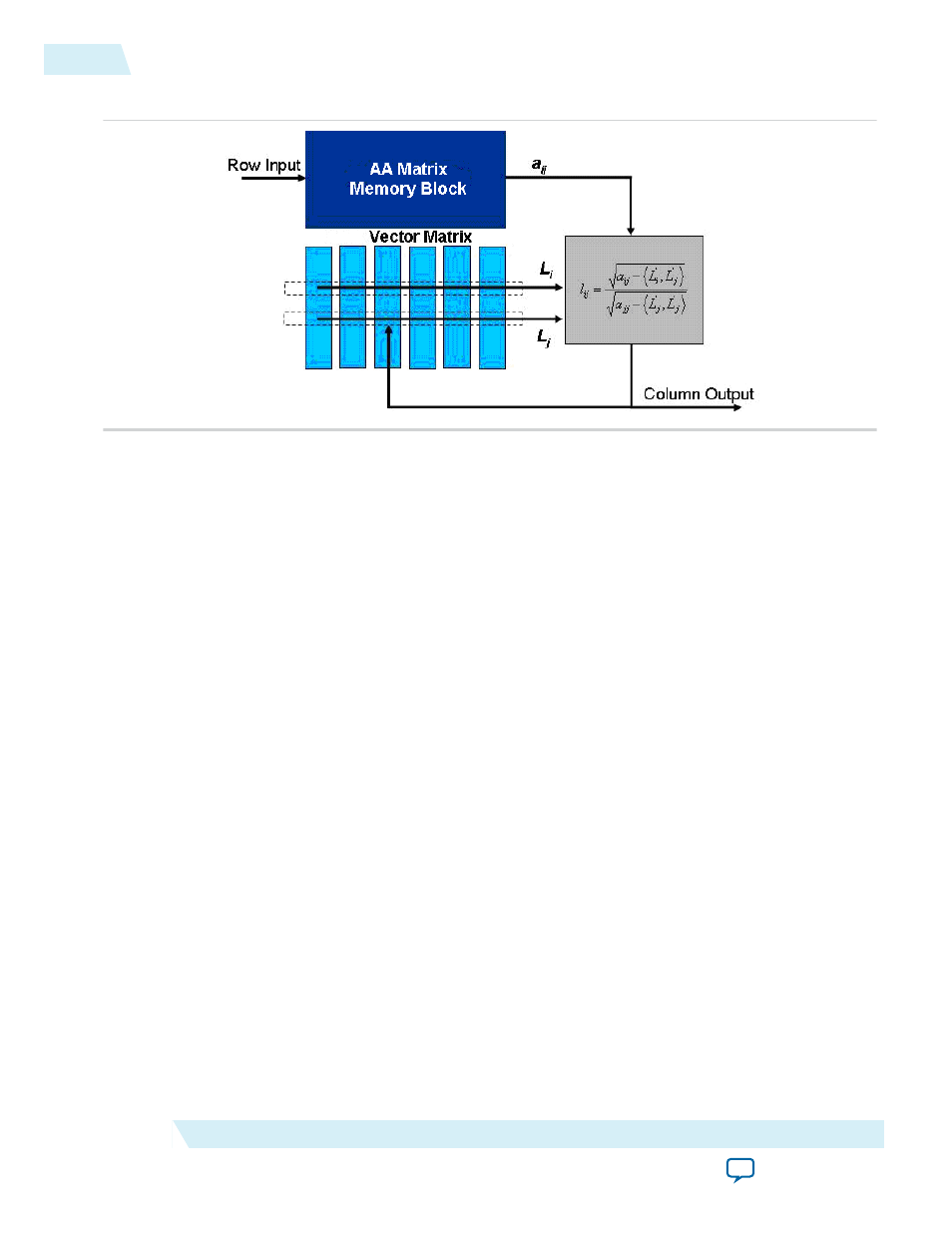
Figure 2-2: Cholesky Decomposition Function Top-level Diagram
Although the Cholesky decomposition algorithm only operates on the lower triangular matrix, the core
requires the entire matrix to be loaded, during which the processing or vector memory is initialized.
The FPC datapath is split into two sections. The first section, also known as the vector section, takes the
inner product of two vectors and subtracts it from the input matrix element, a
ij
. The second section, also
known as the root section, calculates square roots and performs division by the square root. The first
element is loaded into both inputs of the root section and the outcome is its own square root. The first
element continues to stay latched in the left input field of the root section while all the other elements of
the first column are loaded into the right input field. The resulting output is the value of the respective
column element divided by the value of the first element of the Cholesky decomposition matrix.
During processing, two rows from the processing matrix are loaded. For the first element in each new
column, both rows have the same index; hence contain the same values. The first row is latched into the
input register of the vector section. For the rest of the column, the row index is increased, and a new a
ij
element and triangular matrix vector, L
j
is loaded. The first result out of the vector section is latched onto
the left register of the root section. All results from the column, including the first result, are loaded into
the right register of the root section. The root section generates the square root of the first vector result,
while for the other results coming from the vector section, the number is divided by the square root of the
first result.
All calculated values are written to another memory block for further processing. The first column values
are output singly during preprocessing, while the values of other columns are burst out during processing.
There are only minor differences between the architectures for real and complex matrices. For the
complex matrix, both the input and processing memory blocks contain complex values. Similarly, all
values going into the vector section are complex numbers. The complex conjugate of the latched register
is obtained by simply inverting the sign bit. As for the root section, the structure is simplified by the
nature of the positive definite matrix. The diagonal value, which is the first value at the top of each
column in the decomposition, is always a real number so that the result from the inverse square root
calculation is always a real number. The complex multiplier in the root section is therefore a real scalar, so
only two real multipliers are required.
2-4
Cholesky Decomposition Function
UG-01058
2014.12.19
Altera Corporation
ALTERA_FP_MATRIX_INV IP Core
