Altera Floating-Point - Manual (Page 26)

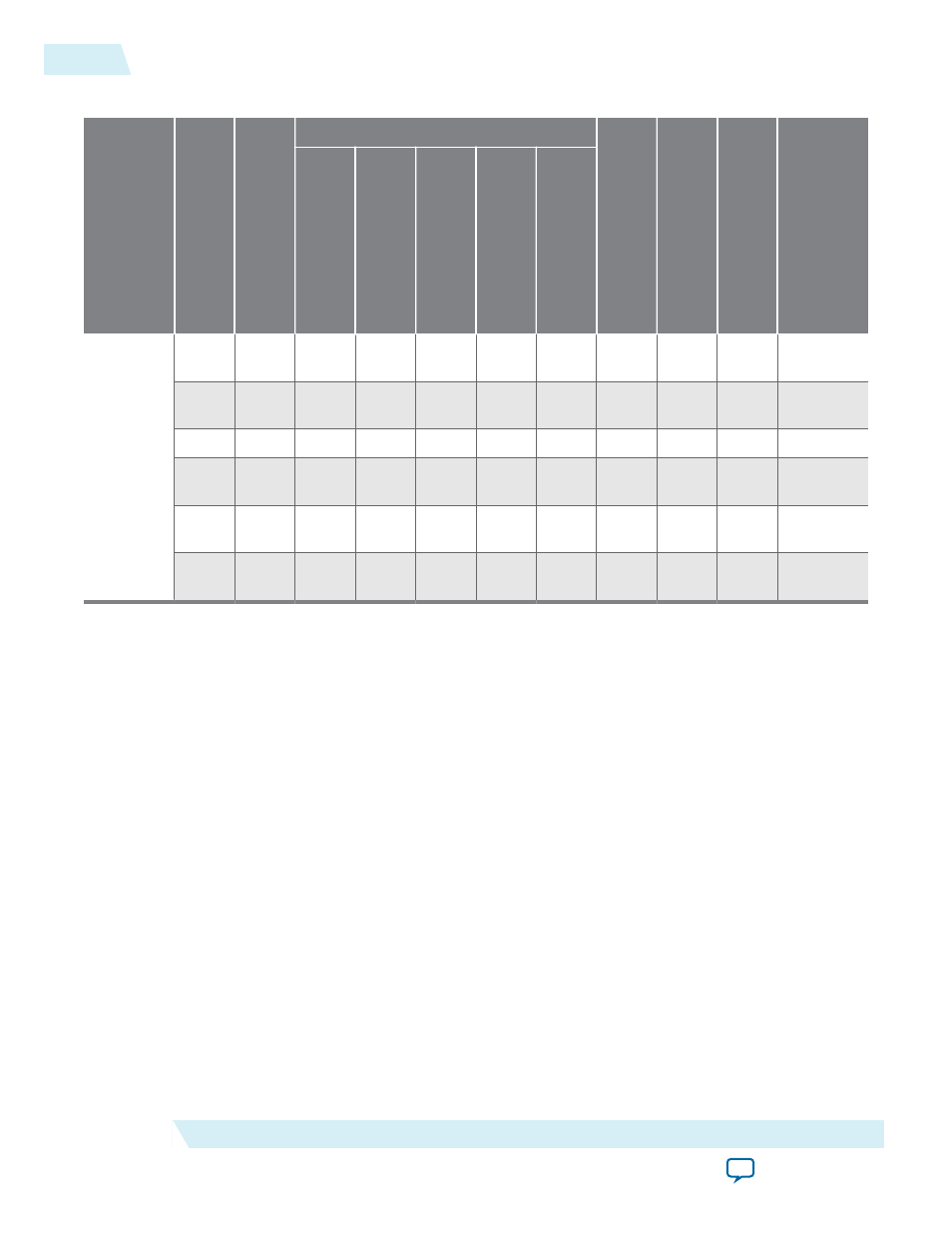
Table 2-1: ALTERA_FP_MATRIX_INV Resource Utilization and Performance for the Stratix IV Device Family
Precision
Matrix
Size
Blocks
Logic usage
Latenc
y
Throug
hput
(kb/s)
Giga
Floatin
g-
Point
Operat
ions
per
Secon
d
(GFLO
PS)
f
MAX
(MHz)
Adapti
ve
Logic
Modul
es
(ALMs)
DSP
Usage
(18 x
18
DSPs)
M9K M144K Memor
y (Bits)
Single
4× 4 2 21159 222 139 — 19919 Pendin
g
Pendin
g
Pendin
g
221
6 × 6 2 59827 574 90 — 15759 Pendin
g
Pendin
g
Pendin
g
170
8 × 8 2 5,538 63 49 — 53,736 2,501 3,987 15.26 332
16 ×
16
4 8,865 95 80 — 138,05
1
11,057 855 30.93 329
32 ×
32
8 15,655 159 193 — 699,16
4
52,625 165 55.12 290
64 ×
64
16 29,940 287 386 22 4,770,3
69
281,50
5
25 83.16 218
ALTERA_FP_MATRIX_INV Functional Description
A matrix inversion function is composed of the following components:
• Cholesky decomposition function.
The Cholesky decomposition function generates a lower triangular matrix.
• Triangular matrix inversion function.
The triangular matrix inversion process then generates the inverse of the lower triangular using
backward substitution.
• Matrix multiplication function.
The matrix multiplier multiplies the transpose of the inverse triangular matrix with the inverse
triangular matrix.
In linear algebra, the Cholesky decomposition states that every positive definite matrix A is decomposed
as A = L×LT
where, L is a lower triangular matrix, and LT denotes the transpose of L.
The property of invertible matrices states that (X×Y)-1 = X-1×Y-1 and the property of transpose states
that (XT )-1 = (X-1)T. Combining these two properties, the following equation represents a derivation of
a matrix inversion using the Cholesky decomposition method:
A-1 = (L×LT)-1
2-2 ALTERA_FP_MATRIX_INV Functional Description
UG-01058
2014.12.19
Altera Corporation ALTERA_FP_MATRIX_INV IP Core
Send Feedback