HP 50g Graphing Calculator User Manual
Page 749
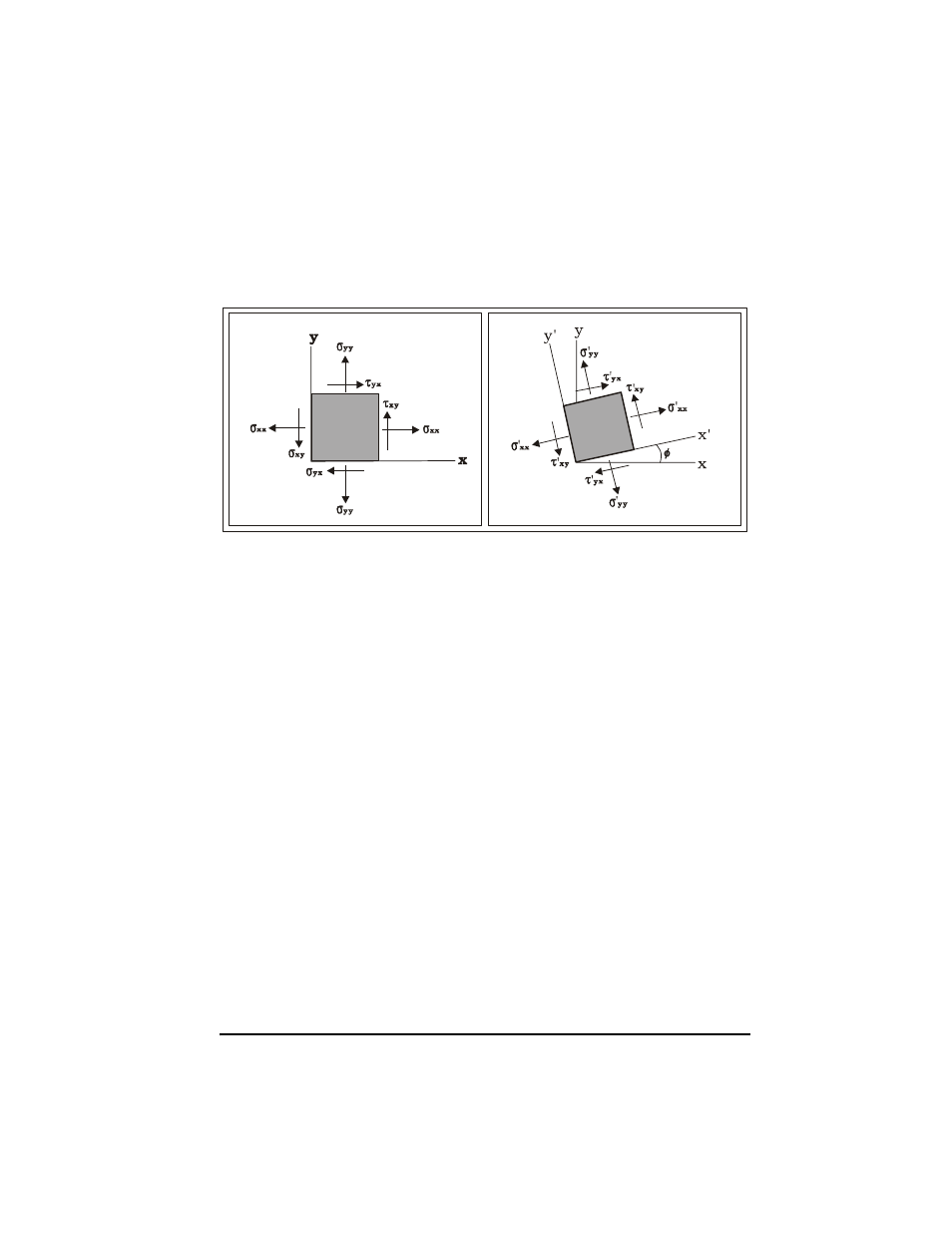
Page 22-34
shows the state of stresses when the element is rotated by an angle
φ. In this
case, the normal stresses are
σ’
xx
and
σ’
yy
, while the shear stresses are
τ’
xy
and
τ’
yx
.
The relationship between the original state of stresses (
σ
xx
,
σ
yy
,
τ
xy
,
τ
yx
) and the
state of stress when the axes are rotated counterclockwise by f (
σ’
xx
,
σ’
yy
,
τ’
xy
,
τ’
yx
), can be represented graphically by the construct shown in the figure below.
To construct Mohr’s circle we use a Cartesian coordinate system with the x-axis
corresponding to the normal stresses (
σ), and the y-axis corresponding to the
shear stresses (
τ). Locate the points A(σ
xx
,
τ
xy
) and B
(σ
yy
,
τ
xy
), and draw the
segment AB. The point C where the segment AB crosses the
σ
n
axis will be the
center of the circle. Notice that the coordinates of point C are (½
⋅(σ
yy
+
σ
xy
),
0). When constructing the circle by hand, you can use a compass to trace the
circle since you know the location of the center C and of two points, A and B.
Let the segment AC represent the x-axis in the original state of stress. If you
want to determine the state of stress for a set of axes x’-y’, rotated
counterclockwise by an angle
φ
with respect to the original set of axes x-y, draw
segment A’B’, centered at C and rotated clockwise by and angle
2φ
with respect
to segment AB. The coordinates of point A’ will give the values (
σ’
xx
,
τ’
xy
), while
those of B’ will give the values (
σ’
yy
,
τ’
xy
).
