HP 50g Graphing Calculator - Manual (Page 523)

Page 16-46
The continuous spectrum, F( ω), is calculated with the integral:
This result can be rationalized by multiplying numerator and denominator by
the conjugate of the denominator, namely, 1-i
ω. The result is now:
which is a complex function.
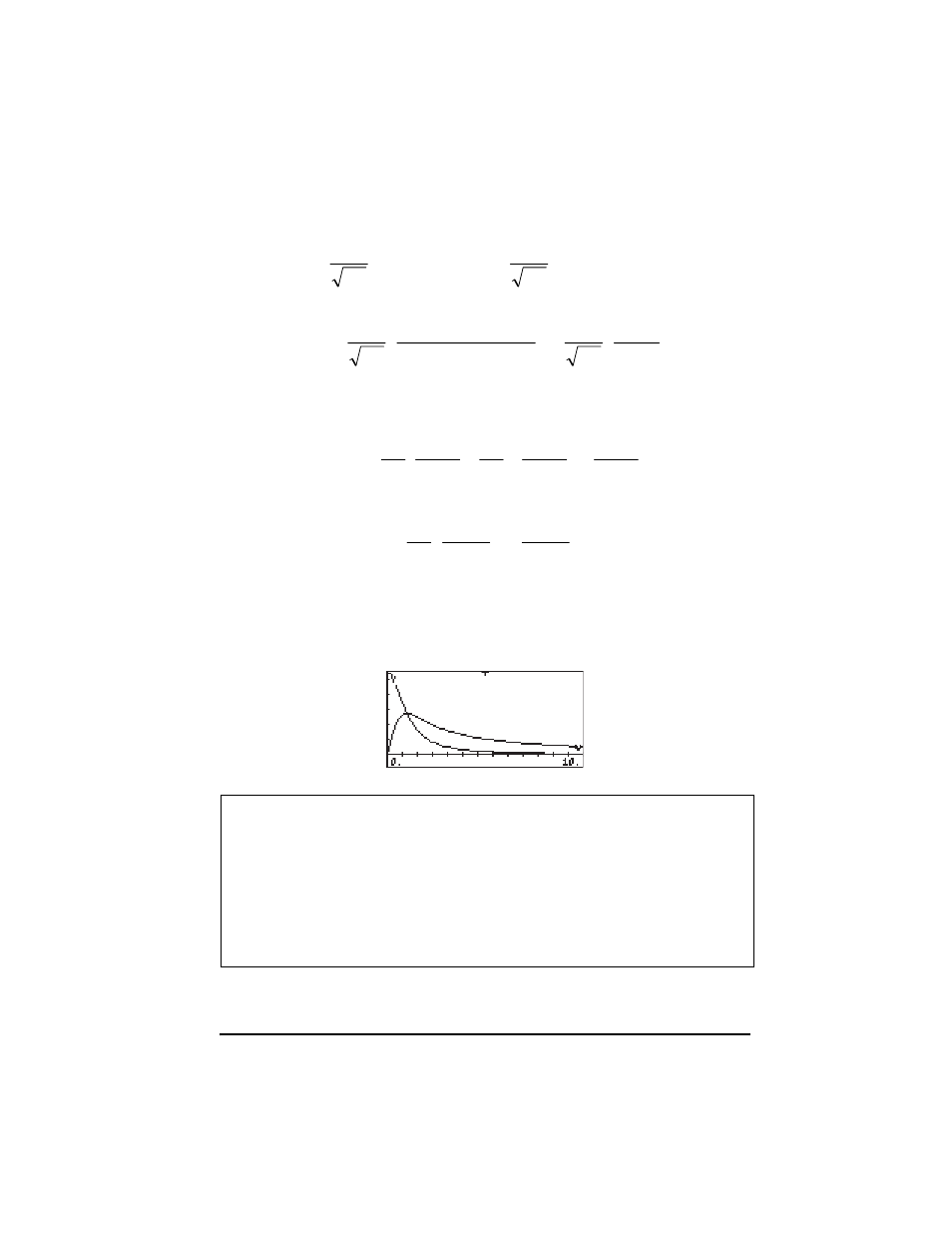
The absolute value of the real and imaginary parts of the function can be
plotted as shown below
Notes:
The magnitude, or absolute value, of the Fourier transform, |F(
ω)|, is the
frequency spectrum of the original function f(t). For the example shown above,
|F(
ω)| = 1/[2π(1+ω 2
)]
1/2
. The plot of |F( ω)| vs. ω was shown earlier.
Some functions, such as constant values, sin x, exp(x), x
2
, etc., do not have
Fourier transform. Functions that go to zero sufficiently fast as x goes to infinity
do have Fourier transforms.
∫ ∫ + −
∞
∞ →
+ − =
ε
ω
ε
ω
π π 0
) 1 (
0
) 1 (
2
1
lim
2
1
dt e dt e
t i t i
.
1
1
2
1
1
) ) 1 ( exp( 1
2
1
lim
ω π ω
ω
π ε i i
t i
+
⋅ =
⎥⎦
⎤
⎢⎣
⎡
+
+ − −
=
∞ →
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅ ⎟
⎠
⎞
⎜
⎝
⎛
+
⋅ =
+
⋅ =
ω
ω
ω π ω π
ω
i
i
i i
F
1
1
1
1
2
1
1
1
2
1
) (
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅ −
+
=
2 2 1 1
1
2
1
ω
ω
ω π
i