HP 50g Graphing Calculator - Manual (Page 473)

Page 15-3
as the matrix H = [h
ij
] = [ ∂φ/∂x
i
∂x
j
], the gradient of the function with respect to
the n-variables, grad f = [ ∂φ/∂x
1
, ∂φ/∂x
2
, … ∂φ/∂x
n
], and the list of
variables [‘x
1
’ ‘x
2
’…’x
n
’]. Consider as an example the function φ(X,Y,Z) = X 2
+
XY + XZ, we’ll apply function HESS to this scalar field in the following example
in RPN mode:
Thus, the gradient is [2X+Y+Z, X, X]. Alternatively, one can use function DERIV
as follows: DERIV(X^2+X*Y+X*Z,[X,Y,Z]), to obtain the same result.
Potential of a gradient
Given the vector field, F(x,y,z) = f(x,y,z)i+g(x,y,z)j+h(x,y,z)k, if there exists a
function
φ(x,y,z), such that f = ∂φ/∂x, g = ∂φ/∂y, and h = ∂φ/∂z, then φ(x,y,z) is
referred to as the potential function for the vector field F. It follows that F = grad
φ = ∇φ.
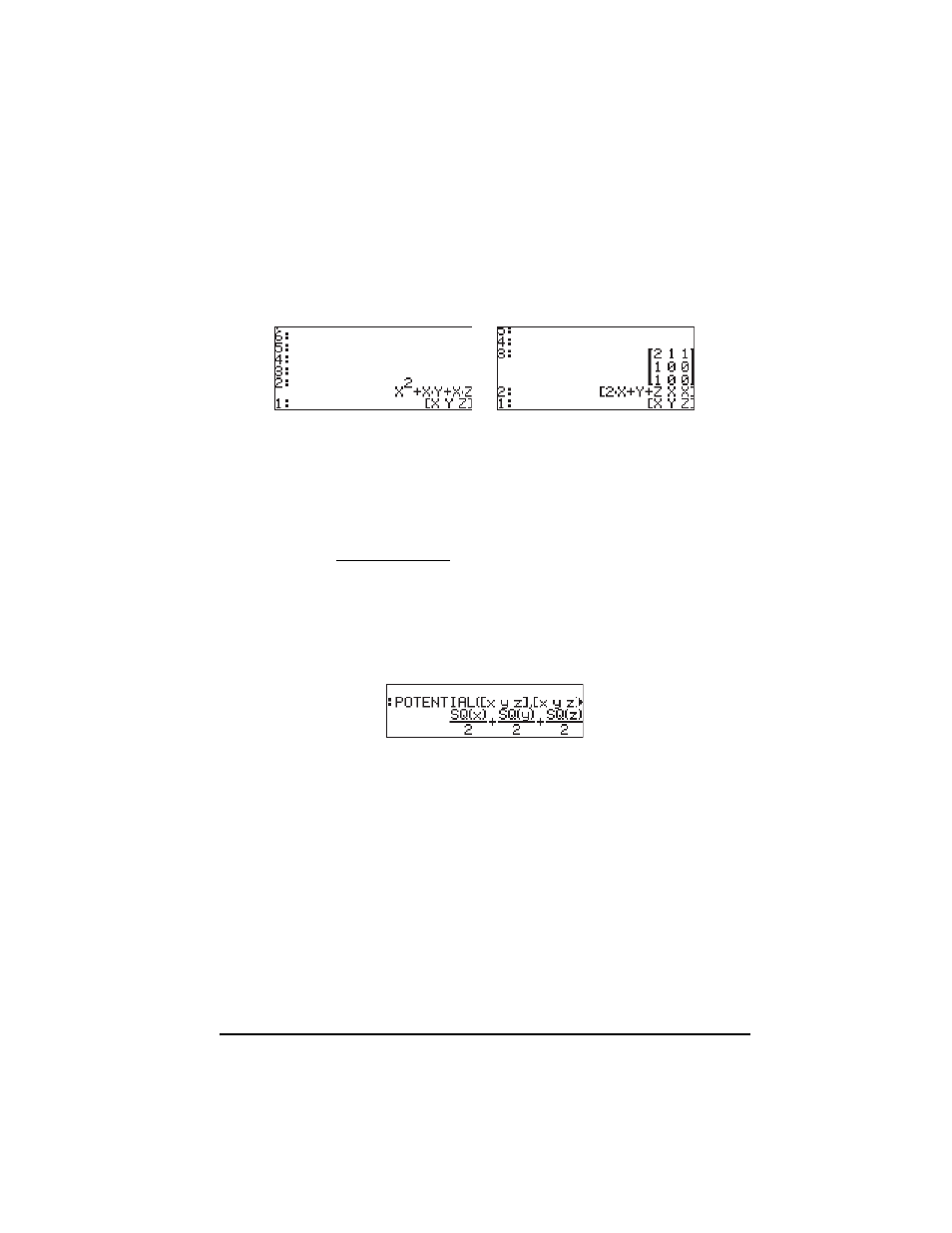
The calculator provides function POTENTIAL, available through the command
catalog (
‚N), to calculate the potential function of a vector field, if it
exists. For example, if F(x,y,z) = xi + yj + zk, applying function POTENTIAL we
find:
Since function SQ(x) represents x
2
, this results indicates that the potential
function for the vector field F(x,y,z) = xi + yj + zk, is φ(x,y,z) = (x 2
+y
2
+z
2
)/2.
Notice that the conditions for the existence of φ(x,y,z), namely, f = ∂φ/∂x, g =
∂φ/∂y, and h = ∂φ/∂z, are equivalent to the conditions: ∂f/∂y = ∂g/∂x, ∂f/∂z =
∂h/∂x, and ∂g/∂z = ∂h/∂y. These conditions provide a quick way to determine
if the vector field has an associated potential function. If one of the conditions
∂f/∂y = ∂g/∂x, ∂f/∂z = ∂h/∂x, ∂g/∂z = ∂h/∂y, fails, a potential function
φ(x,y,z) does not exist. In such case, function POTENTIAL returns an error
message. For example, the vector field F(x,y,z) = (x+y)i + (x-y+z)j + xzk, does