HP 50g Graphing Calculator - Manual (Page 538)

Page 16-61
LL@)PICT To recover menu and return to PICT environment.
@(X,Y)@
To determine coordinates of any point on the graph.
Use the š™ keys to move the cursor around the plot area. At the bottom of
the screen you will see the coordinates of the cursor as (X,Y), i.e., the calculator
uses X and Y as the default names for the horizontal and vertical axes,
respectively. Press
L@CANCL to recover the menu and return to the PLOT
WINDOW environment. Finally, press $ to return to normal display.
Numerical solution of second-order ODE
Integration of second-order ODEs can be accomplished by defining the solution
as a vector. As an example, suppose that a spring-mass system is subject to a
damping force proportional to its speed, so that the resulting differential
equation is:
or, x" = - 18.75 x - 1.962 x',
subject to the initial conditions, v = x' = 6, x = 0, at t = 0. We want to find x,
x' at t = 2.
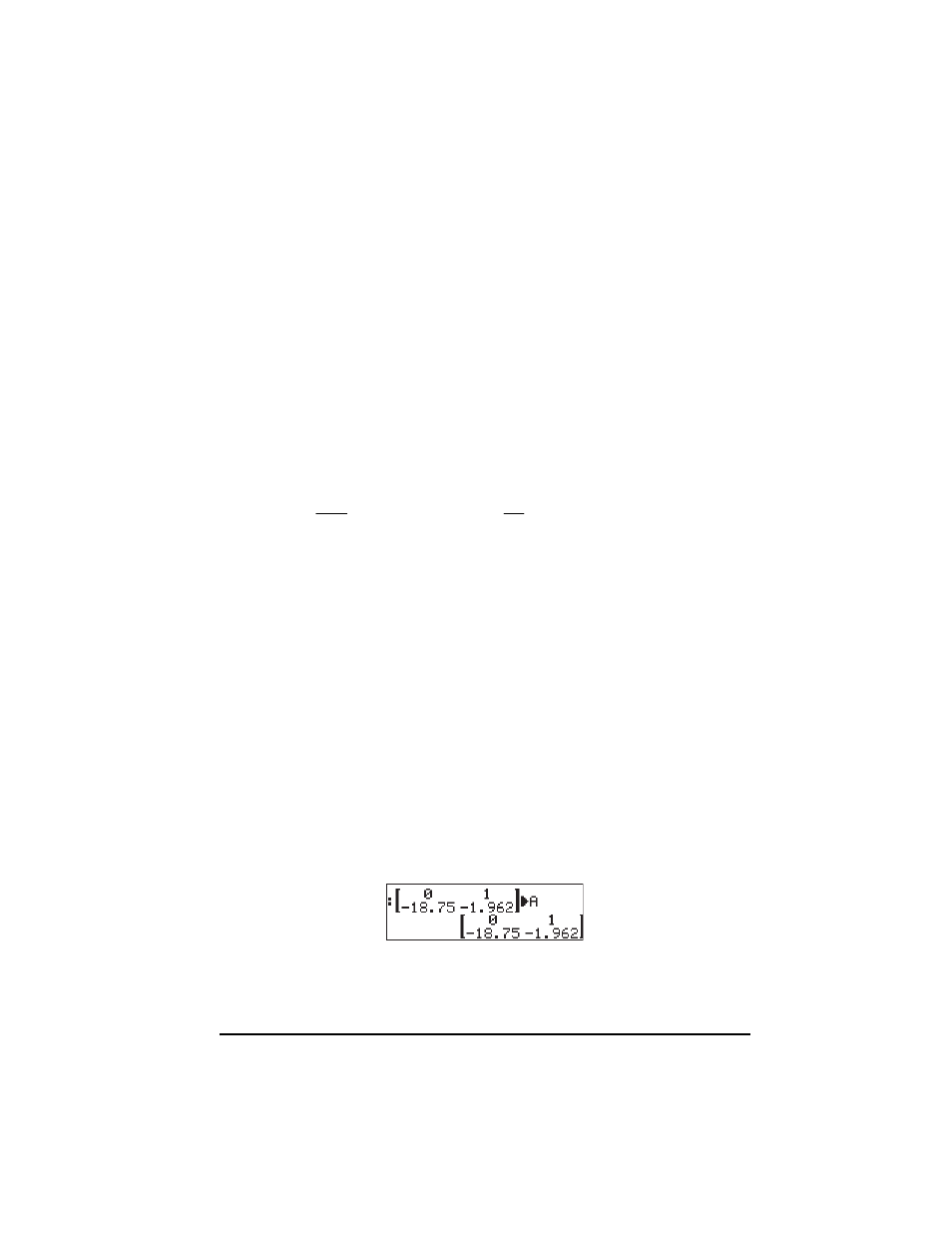
Re-write the ODE as: w' = Aw, where w = [ x x' ]
T
, and A is the 2 x 2 matrix
shown below.
The initial conditions are now written as w = [0 6]
T
, for t = 0. (Note: The
symbol [ ]
T
means the transpose of the vector or matrix).
To solve this problem, first, create and store the matrix A, e.g., in ALG mode:
Then, activate the numerical differential equation solver by using: ‚ Ï
˜ @@@OK@@@ . To solve the differential equation with starting time t = 0 and final
dt
dx
x
dt
x d
⋅ − ⋅ − = 962 . 1 75 . 18
2
2
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎥
⎦
⎤
⎢
⎣
⎡
− −
=
⎥
⎦
⎤
⎢
⎣
⎡
' 962 . 1 75 . 18
1 0
'
'
x
x
x
x