Vicor VI-J00 Family DC-DC Converters and Configurable Power Supplies - Manual (Page 62)

Design Guide & Applications Manual
For VI-200 and VI-J00 Family DC-DC Converters and Configurable Power Supplies
VI-200 and VI-J00 Family Design Guide Rev 3.5 vicorpower.com
Page 61 of 98
Apps. Eng. 800 927.9474 800 735.6200
Temperature differentials encountered in practical
applications of Vicor converters are never large enough
to cause radiational cooling to be the dominant heat
transfer mechanism. Radiation will account for less than
10% of total heat transfer in the majority of cases. For
these reasons, the presence of radiant cooling is often
assumed to provide safety margins over and above the
dominant cooling mechanism, and detailed consideration
of its effects are neglected. A valid assumption, in most
cases, is that the converter will be warmer than its
surroundings and radiant energy transfer will aid cooling.
In some cases, however, nearby objects (PC boards, power
resistors, etc.) may be much hotter than the converter and
net radiant energy transfer may actually increase the
converter’s temperature.
Surveying the relative positions and estimated temperatures
of converters and surrounding parts is advisable as a means
of anticipating the potential effects of radiant transfer. In
cases where hot components are in close proximity to the
converter, the use of interposing barriers can generally
moderate undesirable radiational heating effects.
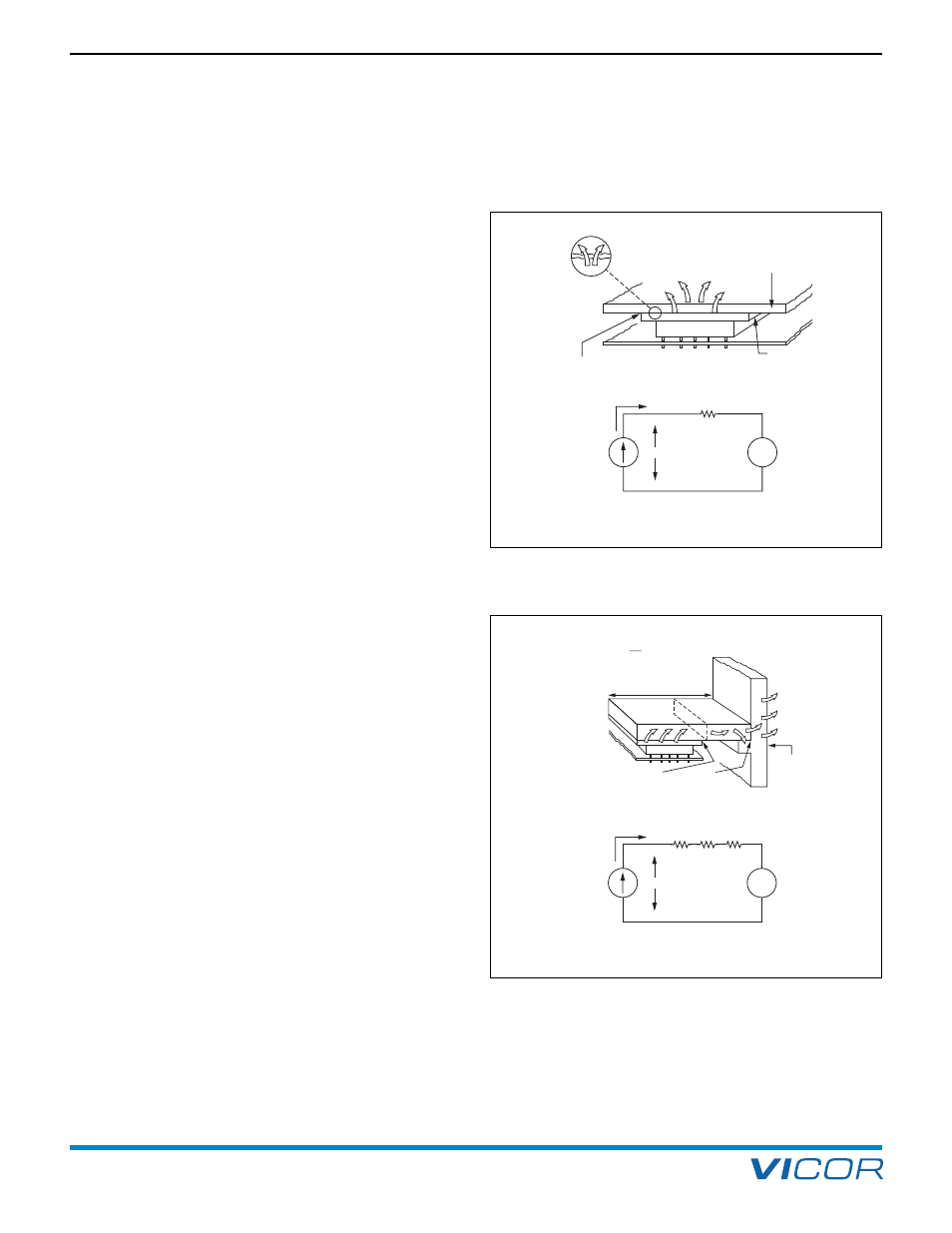
CONDUCTION
In most applications, heat will be conducted from the
baseplate into an attached heat sink or heat conducting
member. Heat conducted across the interface between the
baseplate and mating member will result in a temperature
drop which must be controlled. As shown in Figure 20–2,
the interface can be modeled as a “thermal resistance” in
series with the dissipated power flow. The baseplate
temperature will be the sum of the temperature rise in the
interface and the temperature of the member to which
the baseplate is attached.
Temperature rise across a surface interface can be
significant if not controlled. The area of the interface
should be as large as possible, and the surface flatness of
the attached member should be within 5 mils. Thermal
compound or a thermal pad should be used to fill surface
irregularities. Thermal resistance across surface interfaces
can be held to under 0.1˚C / Watt with proper measures.
Many applications require that heat be conducted from
the baseplate of the converter to a “remote” dissipative
surface via a thermally conductive member. The resulting
baseplate temperature will be the sum of the temperature
of the dissipative surface, the temperature rise in the heat
conducting member, and the rises across the two surface
interfaces. The thermal resistance of the conductive
member is proportional to its length, and inversely
proportional to both its cross-sectional area and thermal
conductivity (Figure 20–3). Minimizing total temperature
rise is dependent on controlling interface resistance, as
described above, and controlling the thermal resistance of
the transfer member through appropriate material
selection and dimensioning.
20. Thermal and Module Mounting Considerations
Baseplate
Heat Flow
Mating Member
at Temperature = Ts
Surface Irregularities
Produce Temperature
Drop in the Interface
θ bs = Interface Thermal Resistance (°C/Watt)
(+)
Tb
(–)
Pdiss
Power
Dissipated
by Converter
(Watts)
Tb = Baseplate Temperature
= Ts + Pdiss x bs
Temperature
of Mating
Surface (°C)
+
Ts
–
bs θ
θ
Figure 20–2 — Baseplate thermal considerations
Figure 20–3 — Interface thermal considerations
Thermal Resistance of Conducting Member ( m)
m =
KA
K = Thermal Conductivity
A = Cross Sectional Area
L = Length
L
bm
Interface
Resistance
ms
Interface
Resistance
Cooling
Surface at
Temperature
= Ts
L
A
θ
θ
θ θ
(+)
Tb
(–)
Pdiss
Power
Dissipated
by Converter
(Watts)
Tb = Baseplate Temperature
= Ts + ( bm + m + ms) x Pdiss
Temperature
of Cooling
Surface (°C)
+
Ts
–
bm ms m θ θ θ
θ θ θ