Texas Instruments PLUS TI-89 User Manual
Page 555
538 Appendix A: Functions and Instructions
8992APPA.DOC TI-89 / TI-92 Plus: Appendix A (US English) Susan Gullord Revised: 02/23/01 1:48 PM Printed: 02/23/01 2:21 PM Page 538 of 132
x
ê
CATALOG (^
-1
)
expression1
x
ê
⇒
expression
list1
x
ê
⇒
list
Returns the reciprocal of the argument.
For a list, returns the reciprocals of the
elements in
list1
.
3.1^ë 1 ¸
.322581
{a,4,ë.1,xм 2}^л 1 ¸
{
1
a
1
4
ë 10.
1
xì 2
}
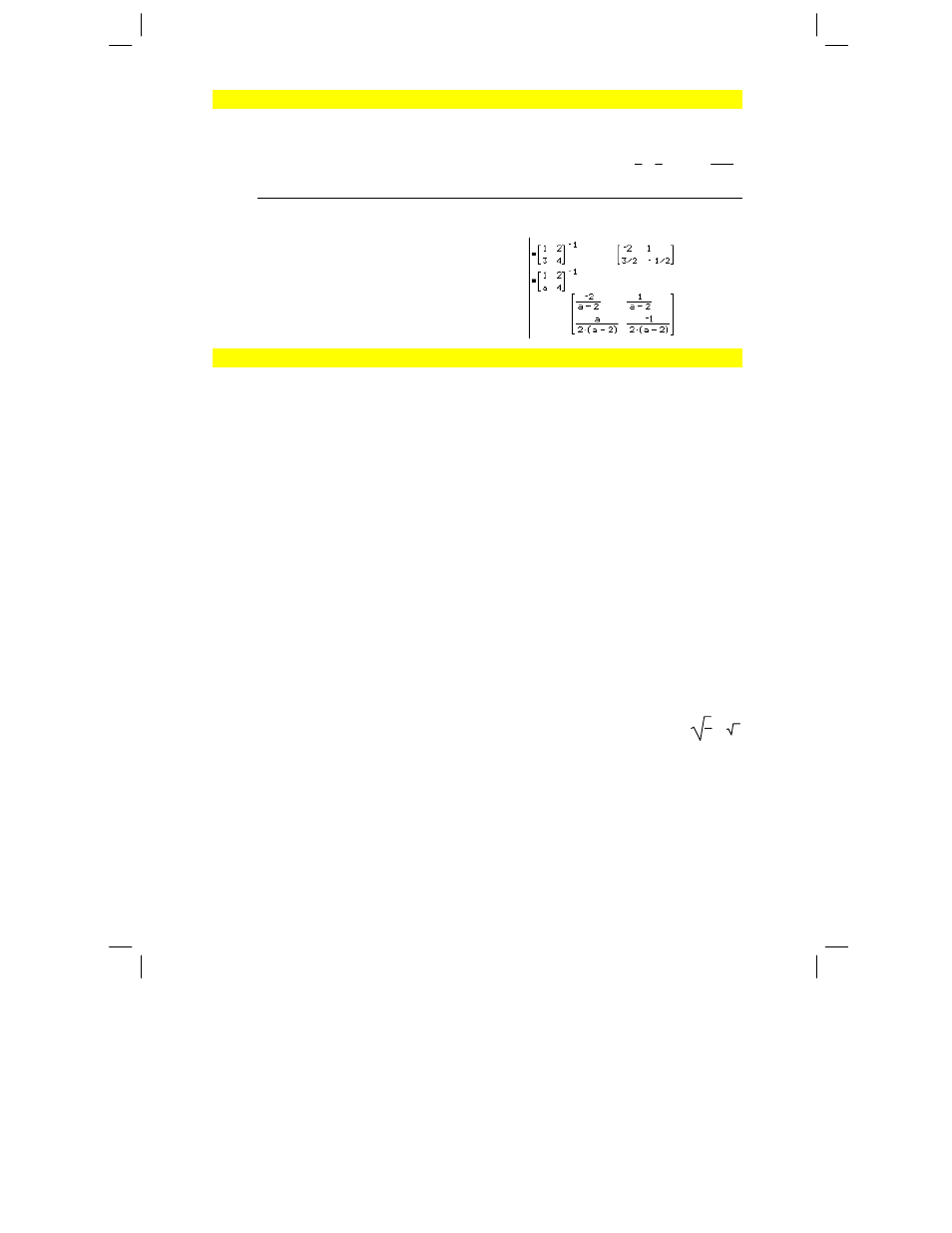
squareMatrix1
x
ê
⇒
squareMatrix
Returns the inverse of
squareMatrix1
.
squareMatrix1
must be a non-singular square
matrix.
[1,2;3,4]^ë 1 ¸
[1,2;a,4]^ë 1 ¸
|
(“with”)
TI
-
89:
Í
key
TI
-
92 Plus:
2
Í
key
expression
|
Boolean expression1 [and Boolean
expression2]...[and Boolean expressionN]
The “with” (|) symbol serves as a binary
operator. The operand to the left of | is an
expression. The operand to the right of |
specifies one or more relations that are
intended to affect the simplification of the
expression. Multiple relations after | must be
joined by a logical “and”.
The “with” operator provides three basic
types of functionality: substitutions, interval
constraints, and exclusions.
x+1| x=3 ¸
4
x+y| x=sin(y) ¸
sin(y) + y
x+y| sin(y)=x ¸
x + y
Substitutions are in the form of an equality,
such as
x=3
or
y=sin(x)
. To be most effective,
the left side should be a simple variable.
expression
|
variable
=
value
will substitute
value
for every occurrence of
variable
in
expression
.
x^3ì 2x+7! f(x) ¸
Done
f(x)| x=
‡(3) ¸
‡3 + 7
(sin(x))^2+2sin(x)ì 6| sin(x)=d
¸
dñ +2dì 6
Interval constraints take the form of one or
more inequalities joined by logical “and”
operators. Interval constraints also permit
simplification that otherwise might be invalid
or not computable.
solve(x^2ì 1=0,x)|x>0 and x<2
¸
x = 1
‡(x)ù ‡(1/x)|x>0 ¸
1
‡(x)ù ‡(1/x) ¸
1
x ø x
Exclusions use the “not equals” (/= or
ƒ)
relational operator to exclude a specific
value from consideration. They are used
primarily to exclude an exact solution when
using
cSolve()
,
cZeros()
,
fMax()
,
fMin()
,
solve()
,
zeros()
, etc.
solve(x^2ì 1=0,x)| x
ƒ1 ¸x = л 1
