Sinreg, Solve() – Texas Instruments PLUS TI-89 User Manual
Page 520
Appendix A: Functions and Instructions 503
8992APPA.DOC TI-89 / TI-92 Plus: Appendix A (US English) Susan Gullord Revised: 02/23/01 1:48 PM Printed: 02/23/01 2:21 PM Page 503 of 132
SinReg
MATH/Statistics/Regressions menu
SinReg
list1
,
list2
[
, [
iterations
]
, [
period
] [,
list3
,
list4
]
]
Calculates the sinusoidal regression and
updates all the system statistics variables.
All the lists must have equal dimensions
except for
list4
.
list1
represents xlist.
list2
represents ylist.
list3
represents category codes.
list4
represents category include list.
iterations
specifies the maximum number of
times (1 through 16) a solution will be
attempted. If omitted, 8 is used. Typically,
larger values result in better accuracy but
longer execution times, and vice versa.
period
specifies an estimated period. If
omitted, the difference between values in
list1
should be equal and in sequential order.
If you specify
period
, the differences between
x values can be unequal.
Note:
list1
through
list3
must be a variable
name or c1–c99 (columns in the last data
variable shown in the Data/Matrix Editor).
list4
does not have to be a variable name and
cannot be c1–c99.
The output of
SinReg
is always in radians,
regardless of the angle mode setting.
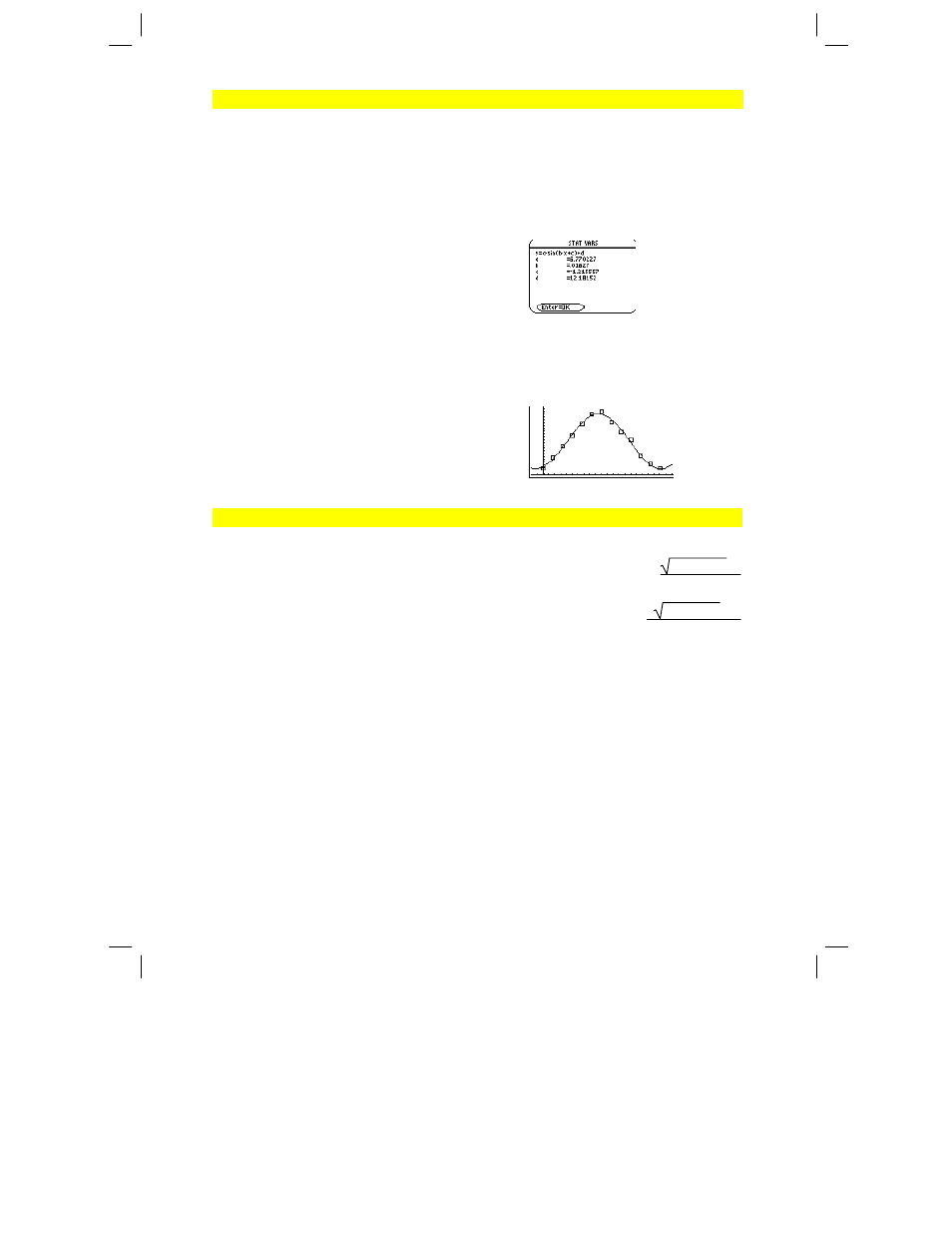
In function graphing mode:
seq(x,x,1,361,30)! L1 ¸
{1 31 61 …}
{5.5,8,11,13.5,16.5,19,19.5,17,
14.5,12.5,8.5,6.5,5.5}! L2 ¸
{5.5 8 11 …}
SinReg L1,L2 ¸
Done
ShowStat ¸
¸
regeq(x)! y1(x) ¸
Done
NewPlot 1,1,L1,L2 ¸
Done
¥ %
„ 9
solve()
MATH/Algebra menu
solve(
equation
,
var
)
⇒
Boolean expression
solve(
inequality
,
var
)
⇒
Boolean expression
Returns candidate real solutions of an equation
or an inequality for
var
. The goal is to return
candidates for all solutions. However, there
might be equations or inequalities for which the
number of solutions is infinite.
solve(aù x^2+bù x+c=0,x) ¸
x =
bс
-4ш aш c-b
2ø a
or x =
ë ( bс -4ш aш c+b)
2ø a
Solution candidates might not be real finite
solutions for some combinations of values for
undefined variables.
ans(1)| a=1 and b=1 and c=1
¸
Error: Non-real result
For the
AUTO
setting of the
Exact/Approx
mode,
the goal is to produce exact solutions when
they are concise, and supplemented by iterative
searches with approximate arithmetic when
exact solutions are impractical.
solve((xì a)e^(x)=ë xù (xì a),x)
¸
x = a or x =ë.567...
Due to default cancellation of the greatest
common divisor from the numerator and
denominator of ratios, solutions might be
solutions only in the limit from one or both
sides.
(x+1)(xì 1)/(xì 1)+xм 3 ¸
2ш xм 2
solve(entry(1)=0,x) ¸
x = 1
entry(2)|ans(1) ¸
undef
limit(entry(3),x,1) ¸
0
For inequalities of types
‚, , <, or >, explicit
solutions are unlikely unless the inequality is
linear and contains only
var
.
solve(5xì 2
‚ 2x,x) ¸
x
‚ 2/3
