Texas Instruments PLUS TI-89 - Manual (Page 140)

Chapter 6: Basic Function Graphing 123
06BASFUN.DOC TI-89/TI-92 Plus: Basic Function Graphing (English) Susan Gullord Revised: 02/23/01 4:09 PM Printed: 02/23/01 4:18 PM Page 123 of 22
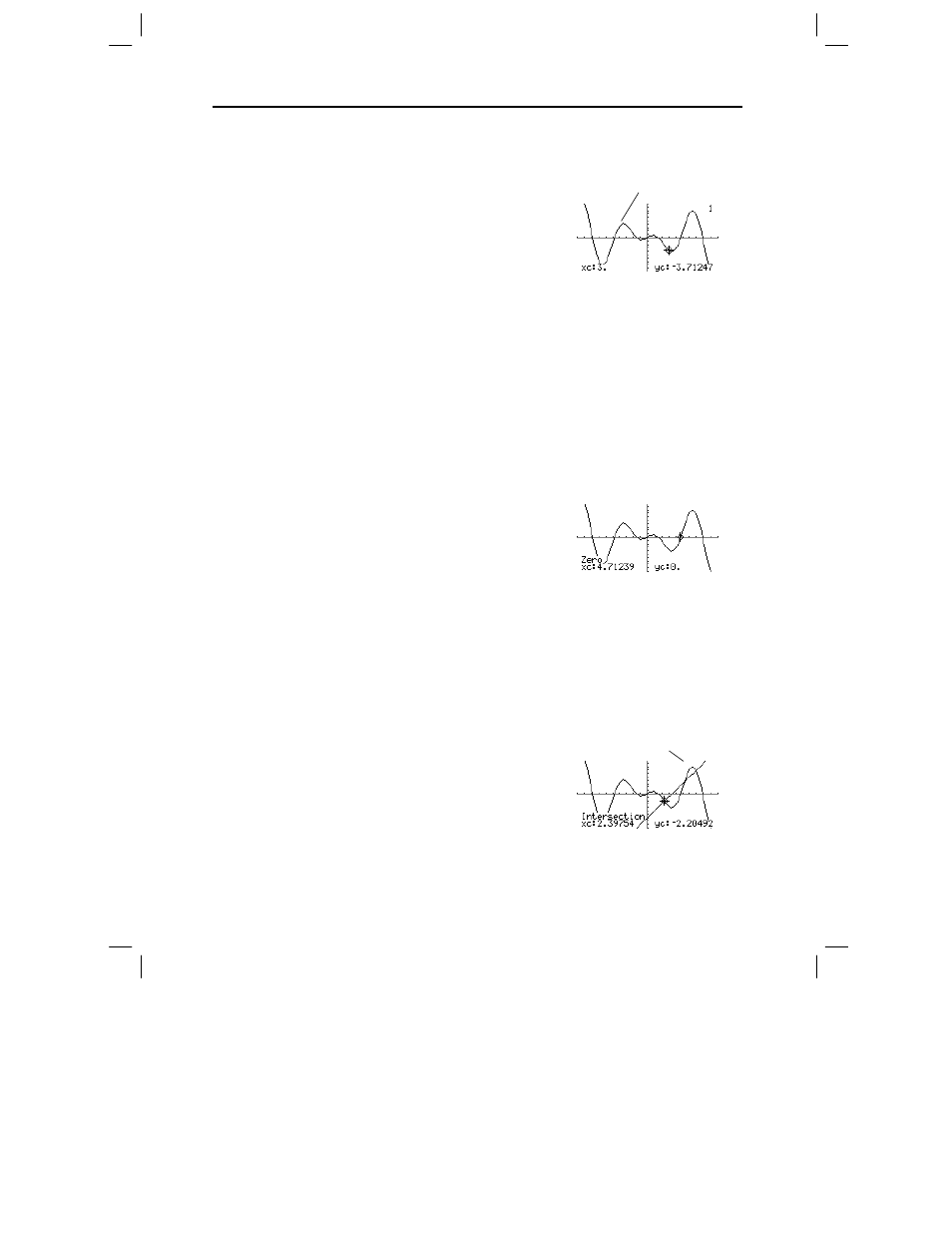
1. From the Graph screen, press ‡ and select 1:Value .
2. Type the x value, which must be a real value between xmin and
xmax . The value can be an expression.
3. Press ¸.
The cursor moves to that
x value on the first function
selected in the Y= Editor, and
its coordinates are displayed.
4. Press D or C to move the cursor between functions at the
entered x value. The corresponding y value is displayed.
Note: If you press A or B, the free-moving cursor appears. You
may not be able to move it back to the entered x value.
1. From the Graph screen, press ‡ and select 2:Zero , 3:Minimum , or
4:Maximum .
2. As necessary, use D and C to select the applicable function.
3. Set the lower bound for x . Either use A and B to move the cursor
to the lower bound or type its x value.
4. Press ¸. A 4 at the top of the screen marks the lower bound.
5. Set the upper bound, and
press ¸.
The cursor moves to the
solution, and its coordinates
are displayed.
1. From the Graph screen, press ‡ and select 5:Intersection .
2. Select the first function, using D or C as necessary, and press
¸. The cursor moves to the next graphed function.
3. Select the second function, and press ¸.
4. Set the lower bound for x . Either use A and B to move the cursor
to the lower bound or type its x value.
5. Press ¸. A 4 at the top of the screen marks the lower bound.
6. Set the upper bound, and
press ¸.
The cursor moves to the
intersection, and its
coordinates are displayed.
Finding y(x) at a
Specified Point
Tip: You can also display
function coordinates by
tracing the function (
… ),
typing an x value, and
pressing
¸ .
Finding a Zero,
Minimum, or
Maximum within an
Interval
Tip: Typing x values is a
quick way to set bounds.
Finding the
Intersection of Two
Functions within an
Interval
y1(x)=1.25x ù cos(x)
y2(x)=2x м 7