Texas Instruments PLUS TI-89 - Manual (Page 204)

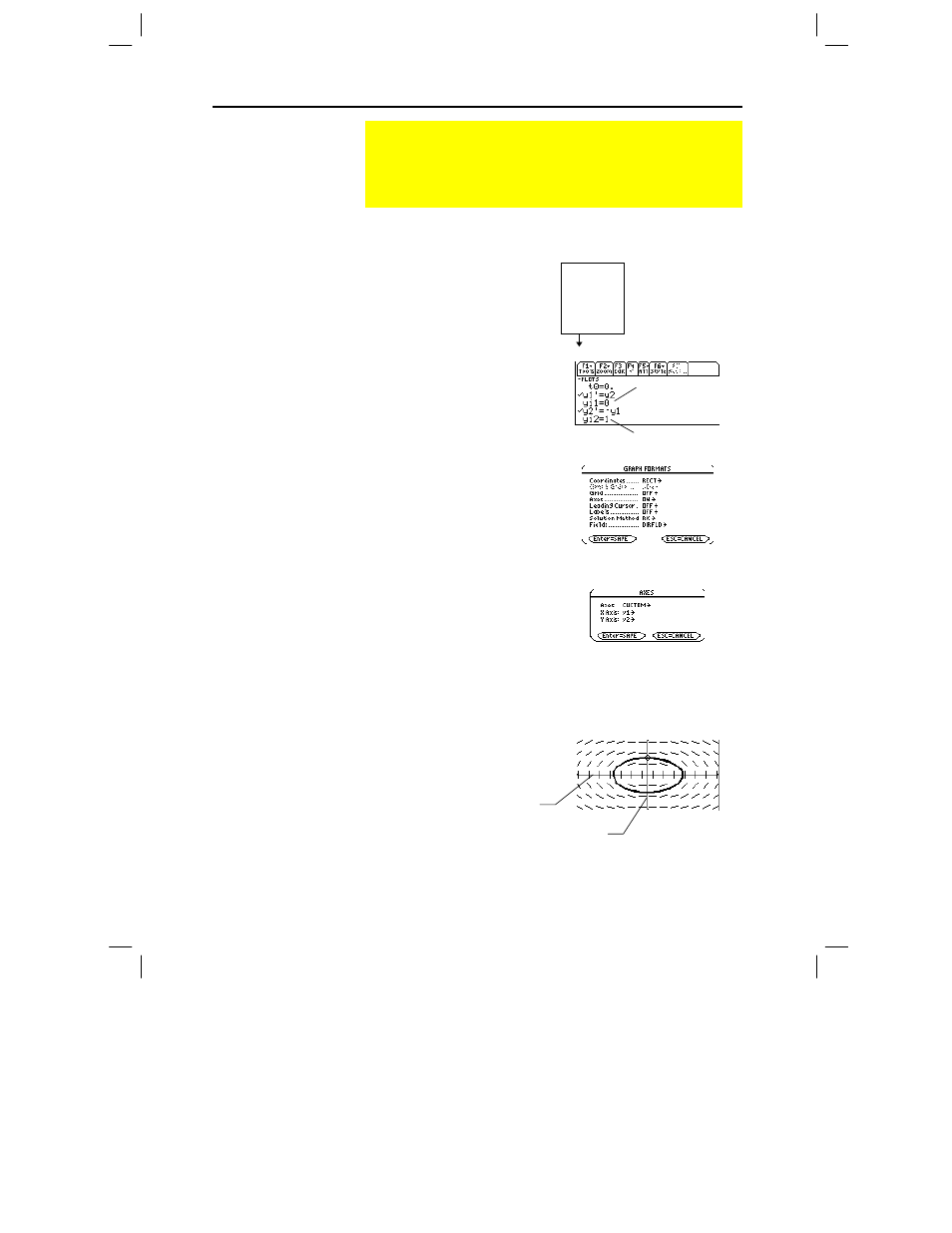
Chapter 11: Differential Equation Graphing 187
11DIFFEQ.DOC TI-89/TI-92 Plus: Differential Equation (English) Susan Gullord Revised: 02/23/01 11:04 AM Printed: 02/23/01 2:15 PM Page 187 of 26
1. Press 3 and set Graph=DIFF EQUATIONS .
2. Define a system of equations
for the 2nd-order equation as
described on page 186.
Rewrite the equation and
make the necessary
substitutions.
3. In the Y= Editor ( ¥ # ),
enter the system of equations.
4. Enter the initial conditions:
yi1=0 and yi2=1
5. Press:
ƒ 9
— or —
TI - 89: ¥ Í
TI - 92 Plus: ¥ F
and set Axes = ON , Labels =
OFF , Solution Method = RK , and
Fields = DIRFLD .
6. In the Y= Editor, press:
TI - 89 : 2 ‰
TI - 92 Plus: ‰
and make sure Axes = CUSTOM
with y1 and y2 as the axes.
7. In the Window Editor
( ¥ $ ), set the
Window variables.
t0=0. xmin= ë 2. ncurves=0.
tmax=10. xmax=2. diftol=.001
tstep=.1 xscl=1. fldres=14.
tplot=0. ymin= ë 2. dtime=0.
ymax=2.
yscl=1.
8. Display the Graph screen
( ¥ % ).
If you select ZoomSqr ( „ 5 ), you can see that the phase-plane orbit
is actually a circle. However, ZoomSqr will change your Window
variables.
Example of a 2nd-Order Equation
The 2nd-order differential equation y''+y = 0 represents a
simple harmonic oscillator. Transform this into a system of
equations for the Y= Editor. Then, graph the solution for initial
conditions y(0) = 0 and y'(0) = 1.
Example
Note: t0 is the time at which
the initial conditions occur. It
is also the first t evaluated
for the graph. By default,
t0=0.
Important: For 2nd-order
equations, you must set
Fields=DIRFLD
or FLDOFF.
Important: Fields=DIRFLD
cannot plot a time axis. An
Invalid Axes
error occurs if
Axes=TIME or if t is set as a
CUSTOM axis.
y'' + y = 0
y'' =
ë y
y'' = ë y1
y2' = ë y1
yi2 is the initial
condition for y'(0).
yi1 is the initial
condition for y(0).
x axis = y1 = y
y axis = y2 = y'