HEIDENHAIN TNC 360 ISO Programming - Manual (Page 141)

7-7 TNC 360
7 Programming with Q Parameters
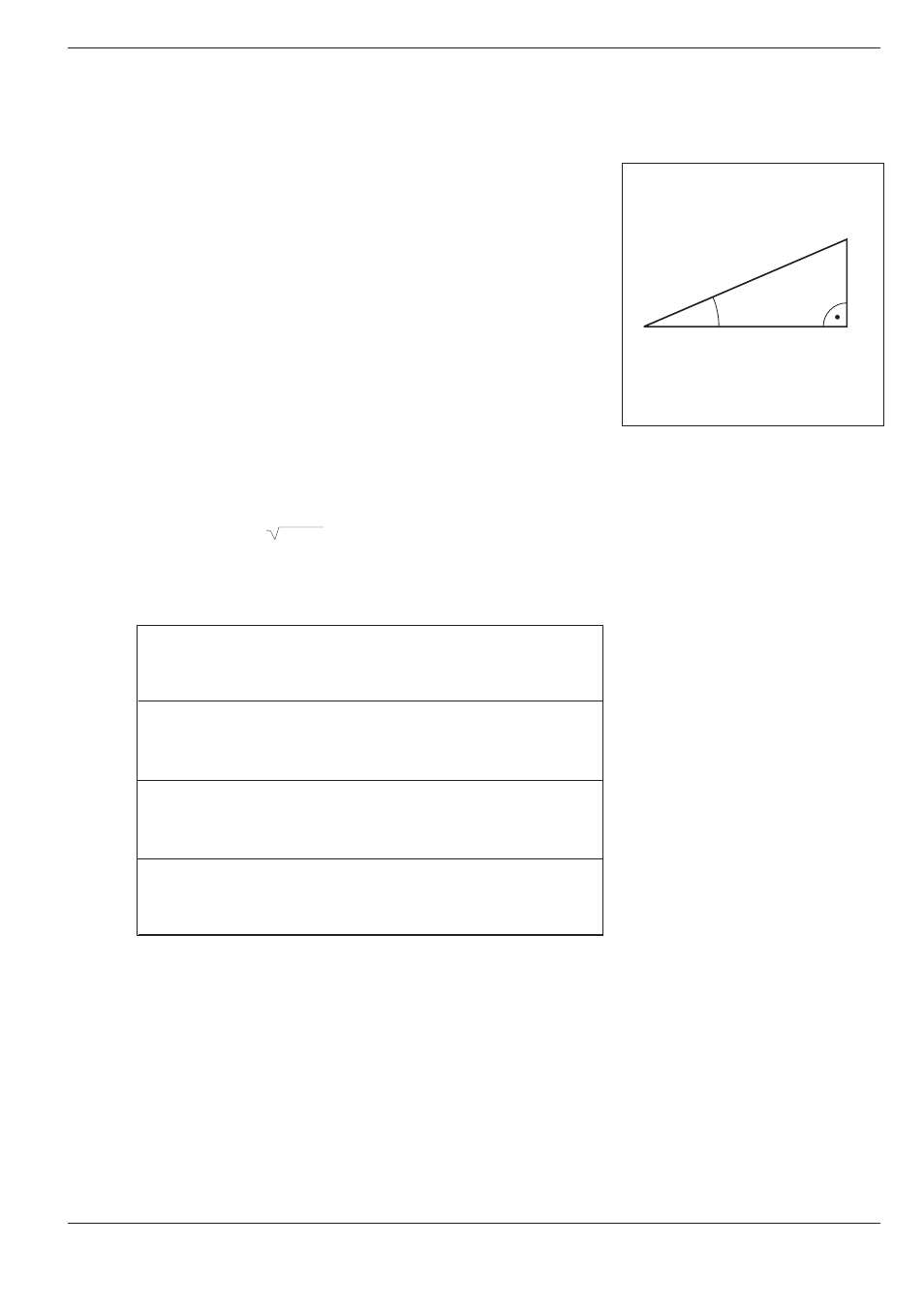
Fig. 7.3: Sides and angles on a right triangle
b
c
a
α
7.3 Trigonometric Functions
Sine, cosine and tangent are the terms for the ratios of the sides of right
triangles. Trigonometric functions simplify many calculations.
For a right triangle,
Sine: sin
α
= a / c
Cosine: cos
α
= b / c
Tangent: tan
α
= a / b = sin
α
/ cos
α
Where
• c is the side opposite the right angle
• a is the side opposite the angle
α
• b is the third side
The angle can be derived from the tangent:
α
= arctan
α
= arctan (a / b) = arctan (sin
α
/ cos
α
)
Example: a = 10 mm
b = 10 mm
α
= arctan (a / b) = arctan 1 = 45°
Furthermore: a 2 + b 2 = c 2 (a 2 = a . a)
c = a 2 + b 2
Overview
D06: SINE
e.g. N10 D06 Q20 P01 –Q05 *
Calculate the sine of an angle in degrees (°) and
assign it to a parameter
D07: COSINE
e.g. N10 D07 Q21 P01 –Q05 *
Calculate the cosine of an angle in degrees (°) and
assign it to a parameter
D08: ROOT SUM OF SQUARES
e.g. N10 D08 Q10 P01 +5 P02 +4 *
Take the square root of the sum of two squares, and
assign it to a parameter
D13: ANGLE
e.g. N10 D13 Q20 P01 +10 P02 –Q01 *
Calculate the angle from the arc tangent of two sides or from
the sine and cosine of the angle, and assign it to a parameter