Banner EZ-SCREEN­ Safety Light Curtain Systems - Manual (Page 61)

P/N 133487
59
Banner Engineering Corp. • Minneapolis, U.S.A.
www.bannerengineering.com • Tel: 763.544.3164
Overview
59
Banner Engineering Corp. • Minneapolis, U.S.A.
www.bannerengineering.com • Tel: 763.544.3164
EZ-SCREEN
Instruction Manual
Cascadeable EZ-SCREEN
7.5 Response Time for Cascaded Light Screens
Response time is an important factor in determining a light
screen’s separation (safety) distance. For cascaded (or
“daisy-chained”) EZ-SCREEN systems, that response time is
dependent on the number of light screens, the number of beams
in the light screens, and their positions in the cascade. It can be
calculated easily, in two ways:
•
Individually for each light screen in the cascade (separation
distance is calculated for each light screen in the cascade), or
• Based on the worst-case time for the entire cascade (all light
screens in the cascade have the same separation distance).
Individual Response Time and Separation Distance
When calculating individual separation distance for each emitter/
receiver pair, the pair’s position in the cascade impacts its
response time, which then impacts its separation distance. This
method results in the closest possible separation distance for
each light screen.
Response time depends on how far “downstream” the light
screen is from the machine control. Each light screen position in
the cascade, starting from the first light screen in the cascade,
increases the light screen’s response time by 2 ms.
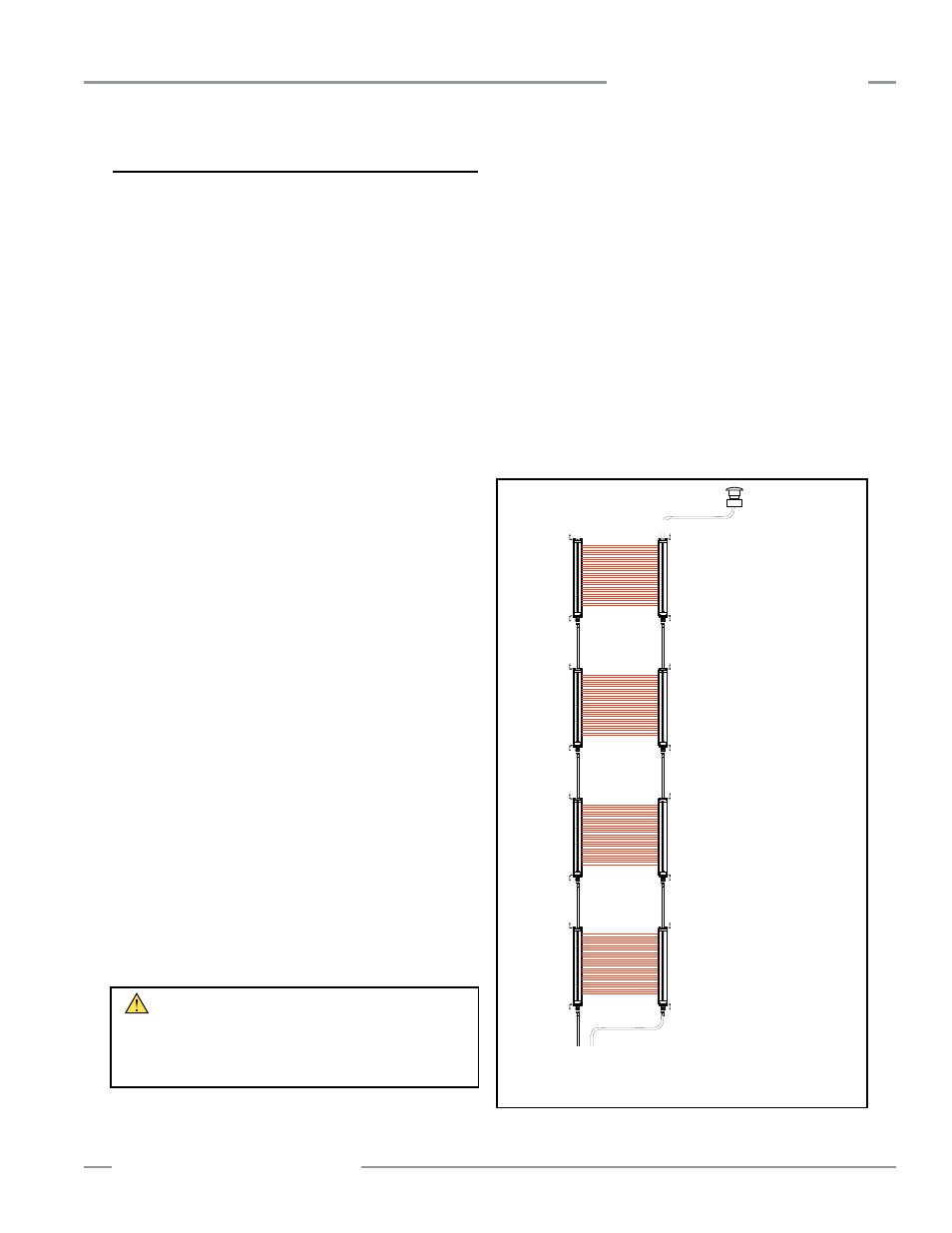
Figure 7-5 depicts a four-pair cascaded system. The 14 mm
resolution, 300 mm EZ-SCREEN emitter/receiver pairs each
begin with a response time of 15 ms. The pair in position #1
(connected directly to the machine control), maintains its
15 ms response time. Response time for the second pair in the
cascade circuit increases by 2 ms, to 17 ms; for the third pair by
4 ms, to 19 ms, and for the fourth pair by 6 ms, to
21 ms. The formula used for U.S. applications (other standards
may apply) to calculate separation distance for individual
placement of each emitter/receiver pair in the cascaded system
is:
Position #1: Ds = K (Ts + Tr) + Dpf
Position #2: Ds = K (Ts + Tr + 2 ms) + Dpf
Position #3: Ds = K (Ts + Tr + 4 ms) + Dpf
Position #4: Ds = K (Ts + Tr + 6 ms) + Dpf
Use the above formulas in place of the Ds formula in Section
3.1.1 to determine individual separation distance (Ds). This will
ensure each sensor pair is located at an adequate distance from
the hazard.
Figure 7-5. Calculating the individual response times of four, 14 mm
resolution, 300 mm cascaded Safety Light Screens
Overall Response Time and Separation Distance
The cascaded system’s Overall Response Time (Tr) is equal
to the response time of the individual sensor pair with the most
beams (i.e., the slowest individual response time), plus an adder
resulting from the number of systems in the cascade. Tr can be
found by the following formula:
Tr = Tr(max) + [(N-1) x 2 ms]
where:
Tr
(max)
is the response time of the slowest individual pair in the
cascade (i.e., the pair with the most beams; see Section 7.2).
N is the number of sensor pairs in the cascade.
Use this Tr value in the formula in Section 3.1.1 to determine
Overall Separation Distance (Ds). This will ensure that all sensor
pairs will be located at an adequate distance from the hazard, no
matter how the system is installed.
WARNING . . .
Proper Installation
The user must comply with all instructions within Section 3 for
proper installation. See Sections 7.2 and 3.1.1 for complete
information.
EZ-SCREEN
Position #3
15 + 2 + 2 = 19
19 ms Response
Emitters Receivers
EZ-SCREEN
Position #4
15 + 2 + 2 + 2 = 21
21 ms Response
E-Stop (CSSI Input)
EZ-SCREEN
Position #2
15 + 2 = 17
17 ms Response
NOTE: Light screens of other lengths/
resolutions will have different
response times.
EZ-SCREEN
Position #1
15 ms Response
NOTE: EZ-SCREEN Cascade
Overall System Response
15 + [(4 – 1) × 2 ms]
15 + 6
21 ms response
Machine
Control
CSSI Response Time = 40 ms + [(4 – 1) × 2 ms] = 46 ms