Instruction 94- pid1 – Maple Systems MAPware-7000 User Manual
Page 153
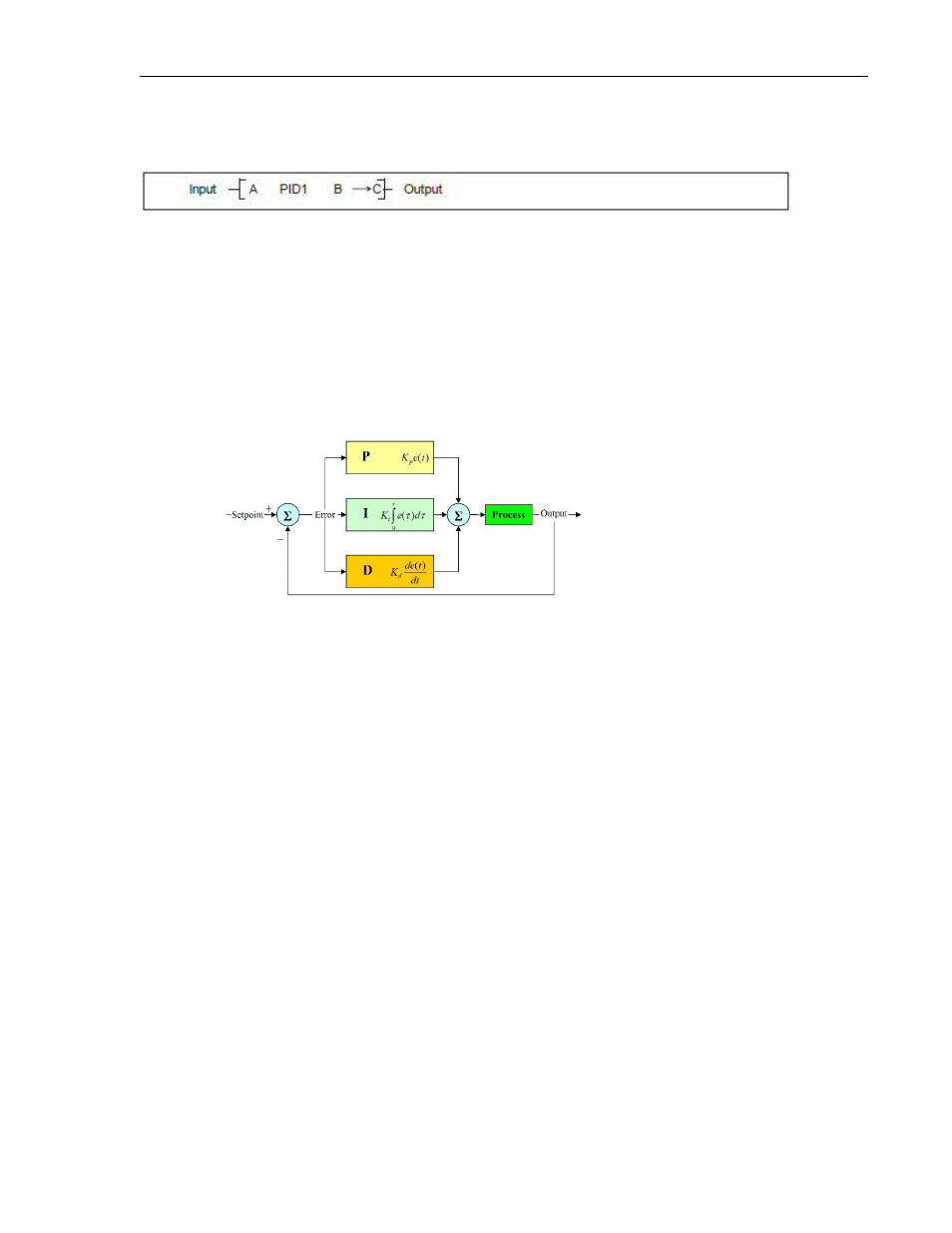
145
MAPware-7000 Ladder Logic Guide
1010-1041 rev. 00
Instruction 94- PID1
Expression:
Space Requirement: 1 line x 6 column Location Requirement: Middle, Right rail
Function:
This function performs a PID (Proportional, Integral, and Derivative) calculation based upon
fourteen input values.
Basically, a PID controller is used to monitor some measureable process
variable in a control system and determine how it varies (the “error” value) from a desired
setpoint. The PID controller then adjusts an input to the control system to minimize the error
value. The name is derived from the three basic mathematical functions that are performed in
order to derive the output:
Generally, the Proportional value tracks the present error, the Integral value tracks the
accumulation of past errors, and the Derivative value predicts future error based upon the
current rate of change. MAPware-7000 provides two PID controller instructions that are based
upon two different formulas.
PID1 is based upon the following formula:
--------P--------|------------------I-----------------|---------------------D-------------------|
M= K
p
* (e-e
-1
) + INT ( | K
il
| * e + I
r
/ |K
ih
|
) + INT [ (|K
dh
| / |K
dl
|) * (2P
-1
-P-P
-2
)]
where:
M= manipulation or control value
Kp = the proportional gain constant
e = deviation or error value
e
-1
= deviation of prior computation
K
ih
= the integral gain constant (high limit value)
K
il
= the integral gain constant (low limit value)
K
dh
= the derivative gain constant (high limit value)
K
dl
= the derivative gain constant (low limit value)
