Inferences concerning two means – HP 48gII User Manual
Page 610
Page 18-39
•
If using z,
P-value = UTPN(0,1,z
o
)
•
If using t,
P-value = UTPT(
ν,t
o
)
Example 2 -- Test the null hypothesis H
o
:
µ = 22.0 ( = µ
o
), against the
alternative hypothesis, H
1
:
µ >22.5 at a level of confidence of 95% i.e., α =
0.05, using a sample of size n = 25 with a mean
x = 22.0 and a standard
deviation s = 3.5. Again, we assume that we don't know the value of the
population standard deviation, therefore, the value of the t statistic is the same
as in the two-sided test case shown above, i.e., t
o
= -0.7142, and P-value, for
ν = 25 - 1 = 24 degrees of freedom is
P-value = UTPT(24, |-0.7142|) = UTPT(24,0.7124) = 0.2409,
since 0.2409 > 0.05, i.e., P-value >
α, we cannot reject the null hypothesis
H
o
:
µ = 22.0.
Inferences concerning two means
The null hypothesis to be tested is H
o
:
µ
1
-
µ
2
=
δ, at a level of confidence (1-
α)100%, or significance level α, using two samples of sizes, n
1
and n
2
, mean
values
x
1
and
x
2
, and standard deviations s
1
and s
2
. If the populations
standard deviations corresponding to the samples,
σ
1
and
σ
2
, are known, or
if n
1
> 30 and n
2
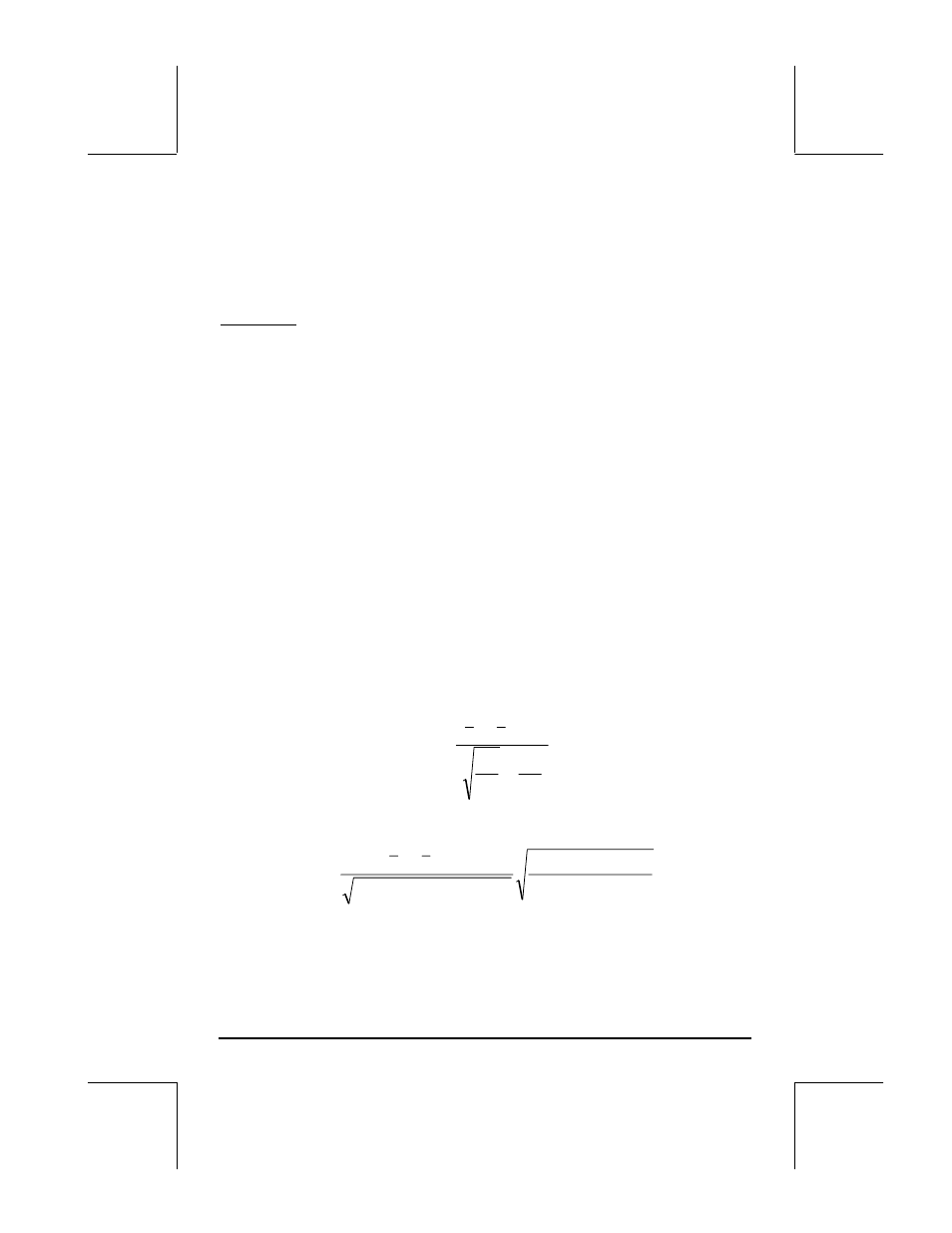
> 30 (large samples), the test statistic to be used is
2
2
2
1
2
1
2
1
)
(
n
n
x
x
z
o
σ
σ
δ
+
−
−
=
If n
1
< 30 or n
2
< 30 (at least one small sample), use the following test statistic:
2
1
2
1
2
1
2
2
2
2
1
1
2
1
)
2
(
)
1
(
)
1
(
)
(
n
n
n
n
n
n
s
n
s
n
x
x
t
+
−
+
−
+
−
−
−
=
δ
