HP 48gII - Manual (Page 365)

Page 11-39
To see the intermediate steps in calculating and inverse, just enter the matrix
A from above, and press Y, while keeping the step-by-step option active in
the calculator’s CAS. Use the following:
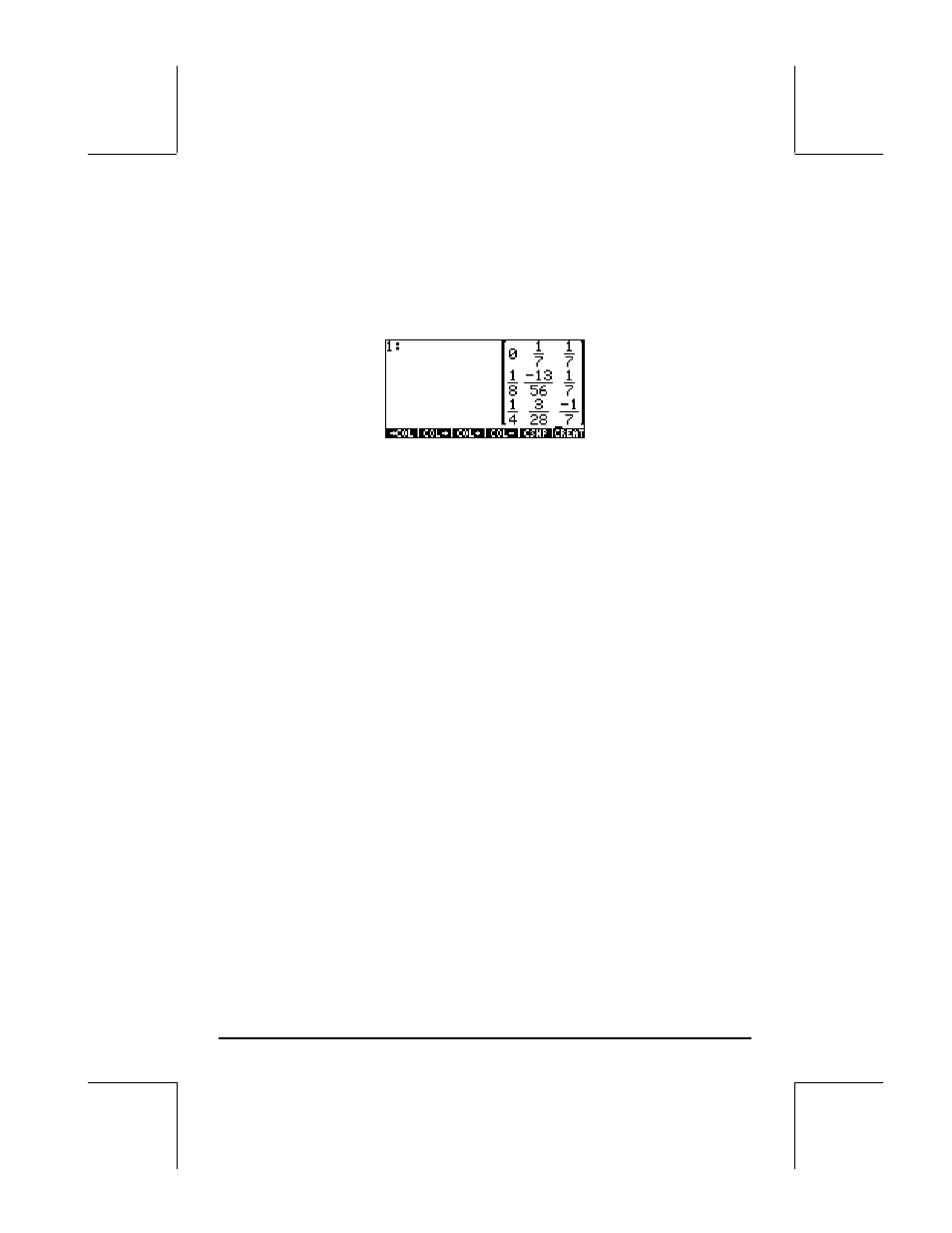
[[ 1,2,3],[3,-2,1],[4,2,-1]] `Y
After going through the different steps, the solution returned is:
What the calculator showed was not exactly a Gauss-Jordan elimination with
full pivoting, but a way to calculate the inverse of a matrix by performing a
Gauss-Jordan elimination, without pivoting. This procedure for calculating
the inverse is based on the augmented matrix (
A
aug
)
n × n
= [ A
n × n
| I
n × n
].
The calculator showed you the steps up to the point in which the left-hand half
of the augmented matrix has been converted to a diagonal matrix. From
there, the final step is to divide each row by the corresponding main diagonal
pivot. In other words, the calculator has transformed (
A
aug
)
n × n
= [ A
n × n
| I
n × n
],
into [ I |A -1 ].
Inverse matrices and determinants
Notice that all the elements in the inverse matrix calculated above are divided
by the value 56 or one of its factors (28, 7, 8, 4 or 1). If you calculate the
determinant of the matrix
A, you get det(A) = 56.
We could write, A -1 = C/det(A), where C is the matrix
.
8 6 14
8 13 7
8 8 0










−
− = C
The result (
A -1 )
n × n
= C
n × n
/det(A
n × n
), is a general result that applies to any non-
singular matrix A. A general form for the elements of C can be written based
on the Gauss-Jordan algorithm.