HP 48gII User Manual
Page 609
Page 18-38
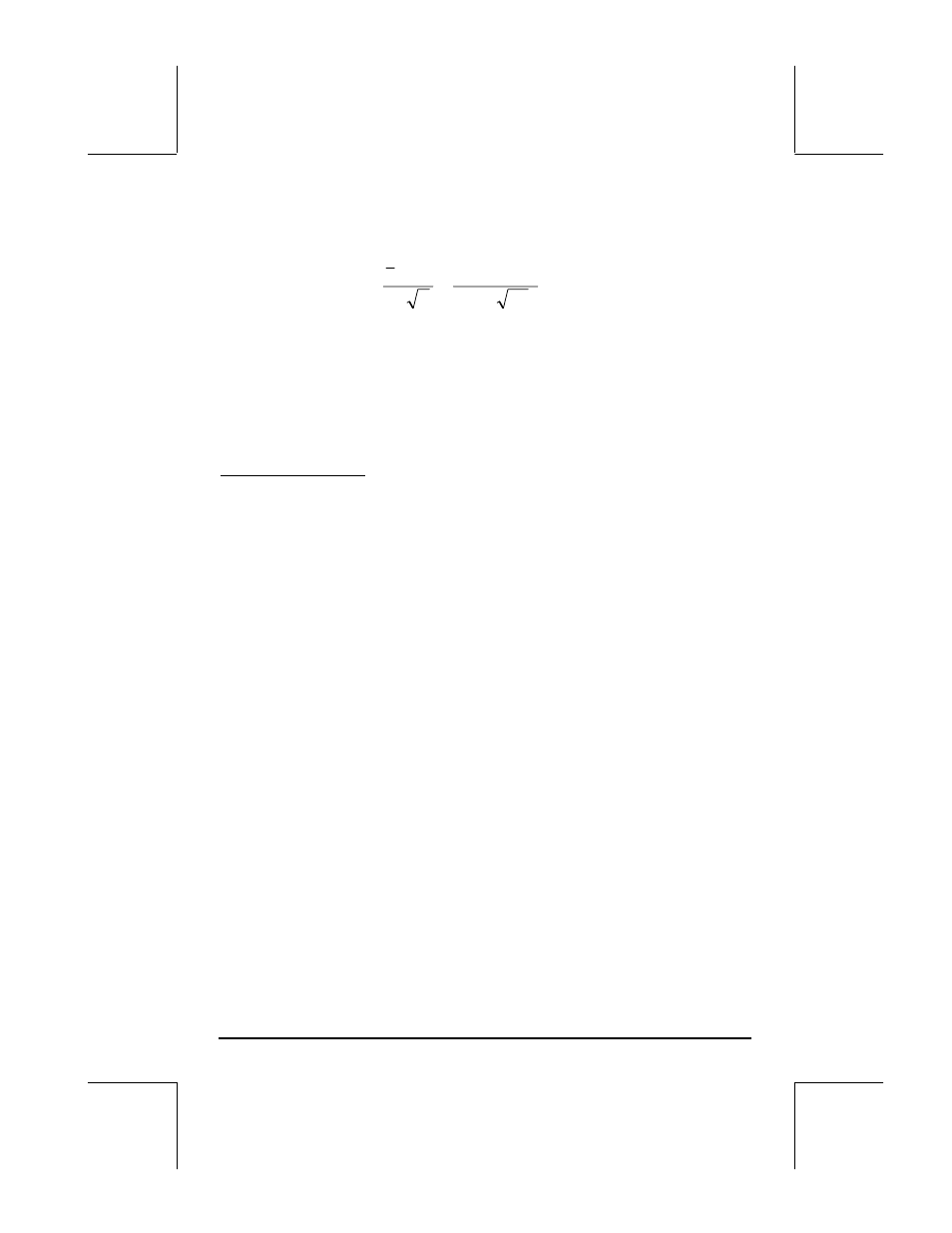
deviation s = 3.5. We assume that we don't know the value of the population
standard deviation, therefore, we calculate a t statistic as follows:
7142
.
0
25
/
5
.
3
5
.
22
0
.
22
/
−
=
−
=
−
=
n
s
x
t
o
o
µ
The corresponding P-value, for n = 25 - 1 = 24 degrees of freedom is
P-value = 2
⋅UTPT(24,-0.7142) = 2⋅0.7590 = 1.5169,
since 1.5169 > 0.05, i.e., P-value >
α, we cannot reject the null hypothesis
H
o
:
µ = 22.0.
One-sided hypothesis
The problem consists in testing the null hypothesis H
o
:
µ = µ
o
, against the
alternative hypothesis, H
1
:
µ > µ
ο
or H
1
:
µ < µ
ο
at a level of confidence (1-
α)100%, or significance level α, using a sample of size n with a mean x and
a standard deviation s. This test is referred to as a one-sided or one-tailed
test. The procedure for performing a one-side test starts as in the two-tailed
test by calculating the appropriate statistic for the test (t
o
or z
o
) as indicated
above.
Next, we use the P-value associated with either z
ο
or t
ο
, and compare it to
α
to decide whether or not to reject the null hypothesis. The P-value for a two-
sided test is defined as either
P-value = P(z > |z
o
|), or, P-value = P(t > |t
o
|).
The criteria to use for hypothesis testing is:
•
Reject H
o
if P-value <
α
•
Do not reject H
o
if P-value >
α.
Notice that the criteria are exactly the same as in the two-sided test. The main
difference is the way that the P-value is calculated. The P-value for a one-
sided test can be calculated using the probability functions in the calculator as
follows:
