HP 48gII User Manual
Page 503
Page 16-25
OBJ
ƒ ƒ
Isolates right-hand side of last expression
ILAP
Obtains the inverse Laplace transform
The result is ‘y1*SIN(X-1)+y0*COS(X-1)-(COS(X-3)-1)*Heaviside(X-3)’.
Thus, we write as the solution: y(t) = y
o
cos t + y
1
sin t + H(t-3)
⋅(1+sin(t-3)).
Check what the solution to the ODE would be if you use the function LDEC:
‘H(X-3)’
`[ENTER] ‘X^2+1’ ` LDEC
The result is:
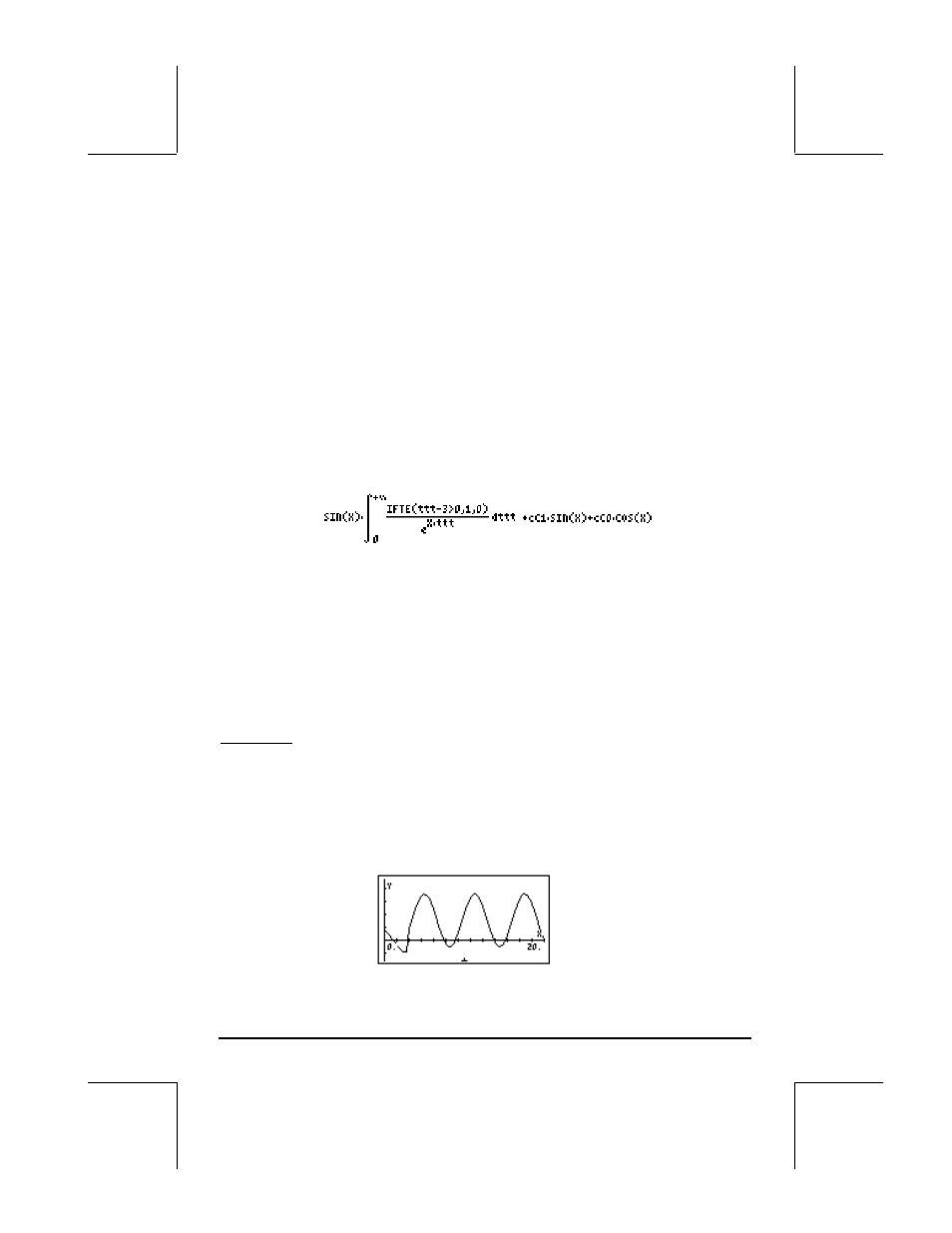
Please notice that the variable X in this expression actually represents the
variable t in the original ODE, and that the variable ttt in this expression is a
dummy variable. Thus, the translation of the solution in paper may be written
as:
Example 4 – Plot the solution to Example 3 using the same values of y
o
and y
1
used in the plot of Example 1, above. We now plot the function
y(t) = 0.5 cos t –0.25 sin t + (1+sin(t-3))
⋅H(t-3).
In the range 0 < t < 20, and changing the vertical range to (-1,3), the graph
should look like this:
.
)
3
(
sin
sin
cos
)
(
0
1
∫
∞
−
⋅
⋅
−
⋅
+
⋅
+
⋅
=
du
e
u
H
t
t
C
t
Co
t
y
ut
