HP 48gII - Manual (Page 468)

Page 14-7
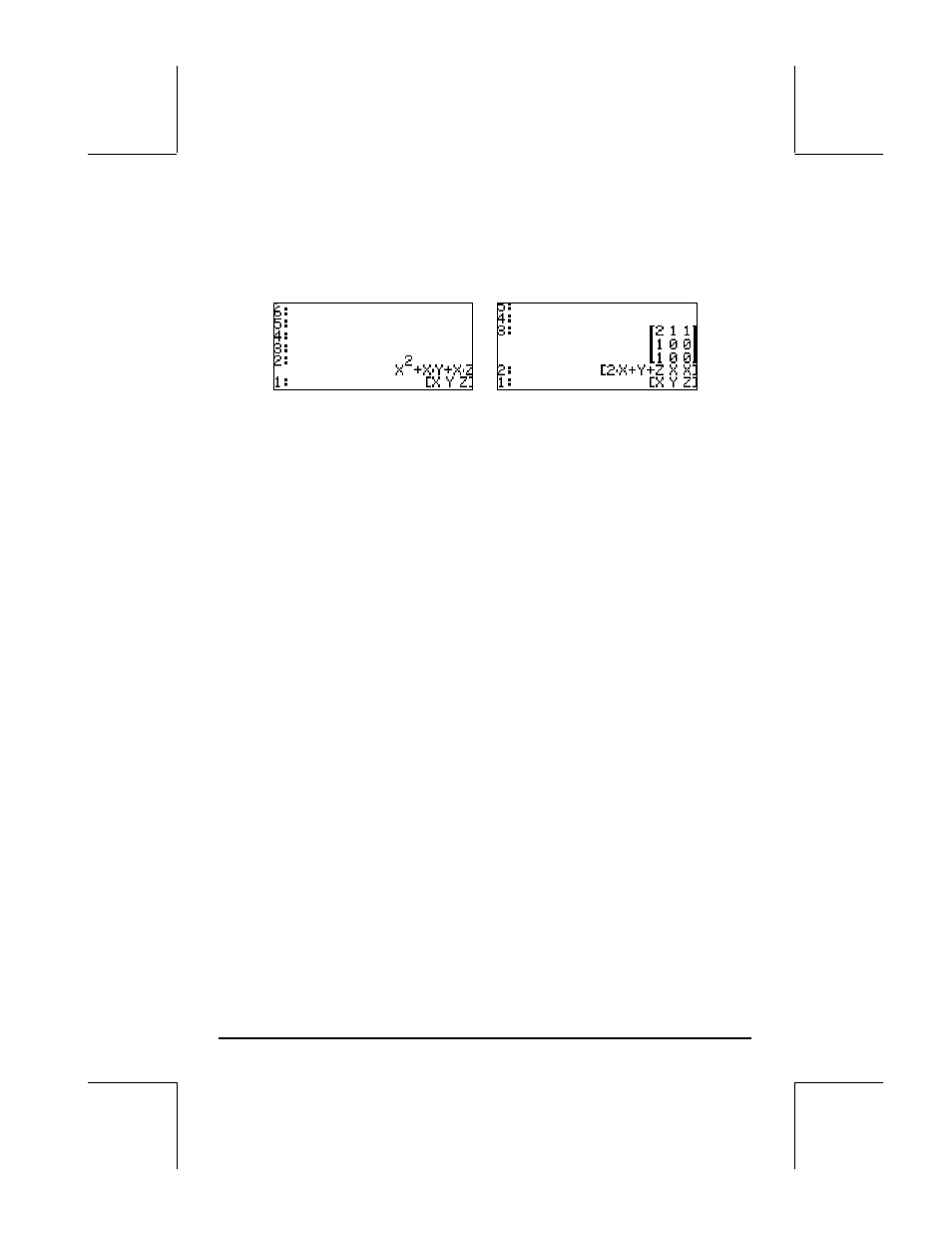
Applications of function HESS are easier to visualize in the RPN mode.
Consider as an example the function
φ(X,Y,Z) = X 2 + XY + XZ, we’ll apply
function HESS to function φ in the following example. The screen shots show
the RPN stack before and after applying function HESS.
When applied to a function of two variables, the gradient in level 2, when
made equal to zero, represents the equations for critical points, i.e.,
∂φ/∂x
i
=
0, while the matrix in level 3 represent second derivatives. Thus, the results
from the HESS function can be used to analyze extrema in functions of two
variables. For example, for the function f(X,Y) = X
3 -3X-Y 2 +5, proceed as
follows in RPN mode:
‘X^3-3*X-Y^2+5’
` [‘X’,’Y’] ` Enter function and variables
HESS Apply function HESS
SOLVE Find critical points
µ Decompose vector
‘s1’ K ‘s2’ K Store critical points
The variables s1 and s2, at this point, contain the vectors [‘X=-1’,’Y=0] and
[‘X=1’,’Y=0], respectively. The Hessian matrix is at level 1 at this point.
‘H’
K Store Hessian matrix
J @@@H@@@ @@s1@@ SUBST ‚ï Substitute s1 into H
The resulting matrix A has a
11
elements a
11
= ∂ 2 φ/∂X 2 = -6., a
22
= ∂ 2 φ/∂X 2 = -
2., and a
12
= a
21
= ∂ 2 φ/∂X∂Y = 0. The discriminant, for this critical point
s1(-1,0) is ∆ = (∂ 2
f/ ∂x 2
)
⋅
( ∂ 2
f/ ∂y 2
)-[ ∂ 2
f/ ∂x∂y] 2 = (-6.)(-2.) = 12.0 > 0. Since
∂ 2 φ/∂X 2 <0, point s1 represents a relative maximum.
Next, we substitute the second point, s2, into H:
J @@@H@@@ @@s2@@ SUBST ‚ï
Substitute s2 into H