HP 48gII - Manual (Page 567)

Page 17-14
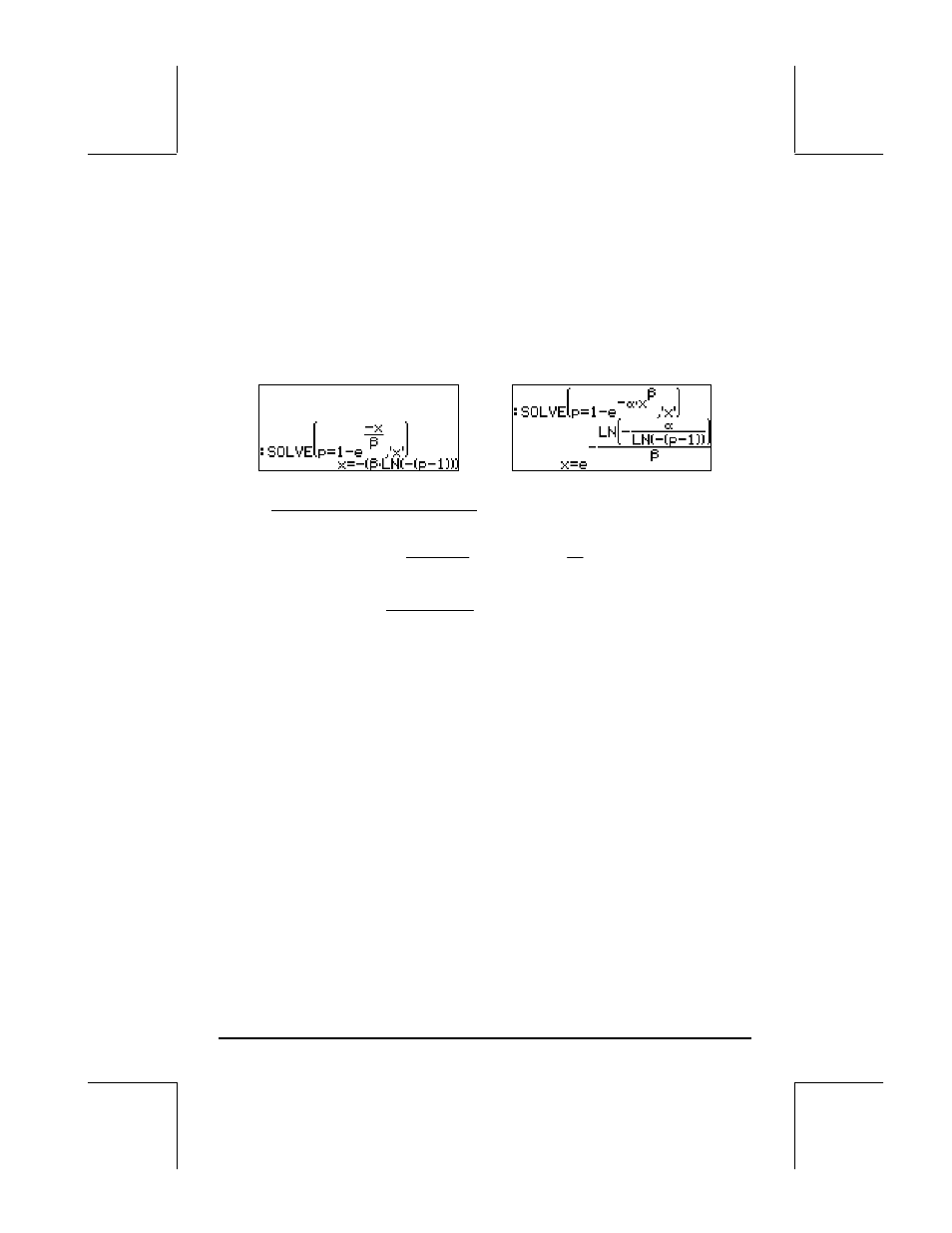
• Exponential, F(x) = 1 - exp(-x/β)
• Weibull, F(x) = 1-exp(-αx
β
)
(Before continuing, make sure to purge variables
α and β). To find the inverse
cdf’s for these two distributions we need just solve for x from these expressions,
i.e.,
Exponential: Weibull:
For the Gamma and Beta distributions the expressions to solve will be more
complicated due to the presence of integrals, i.e.,
• Gamma,
∫ − ⋅ ⋅
Γ
= −
x
dz
z
z p
0
1 ) exp(
) (
1
β α β
α
α
• Beta,
∫ − − − ⋅ ⋅
Γ ⋅ Γ
+ Γ
=
x
dz z z p
0
1 1
) 1 (
) ( ) (
) (
β α
β α
β α
A numerical solution with the numerical solver will not be feasible because of
the integral sign involved in the expression. However, a graphical solution is
possible. Details on how to find the root of a graph are presented in Chapter
12. To ensure numerical results, change the CAS setting to Approx. The
function to plot for the Gamma distribution is
Y(X) = ∫(0,X,z^(α-1)*exp(-z/β)/(β^α*GAMMA(α)),z)-p
For the Beta distribution, the function to plot is
Y(X) =
∫(0,X,z^(α-1)*(1-z)^(β-1)*GAMMA(α+β)/(GAMMA(α)*GAMMA(β)),z)-p
To produce the plot, it is necessary to store values of α, β, and p, before
attempting the plot. For example, for α = 2, β = 3, and p = 0.3, the plot of
Y(X) for the Gamma distribution is shown below. (Please notice that, because